<목차>
1. 표본공간과 사건
1-1. 표본공간과 사건 용어 정의
1-2. 이산 표본공간과 연속 표본공간
1-3. 사건의 연산
* '이공계생을 위한 확률과 통계 2판'을 참고해서 작성한 글입니다.
1. 표본공간과 사건
1-1. 표본공간과 사건 용어 정의
표본공간
- 실험 또는 시행에 의하여 일어날 수 있는 모든 가능한 결과의 집합
예) 동전 던졌을 때 나올 수 있는 전체의 경우의 수.
가령 1개의 동전을 반복해서 2번 던질 때
(앞, 앞), (뒤, 뒤), (앞, 뒤), (뒤, 앞) 총 4개의 경우의 수가 나오고,
이 4개의 경우의 수가 표본공간에 해당한다.
예) 주사위 던졌을 때 나오는 전체 경우의 수
사건
- 표본공간의 임의의 부분집합
예) 동전 전지기 했을 때 나오는 표본공간은 앞, 뒷면이다.
그리고 사건은 앞면이 나올 수 있는 사건과
뒷면이 나올 수 있는 사건으로 나뉠 수 있다.
표본점
- 표본공간을 구성하고 있는 개개의 원소
- 표본점들이 모여서 표본공간을 이룬다.
예) 동전 던지기의 경우, 앞면 혹은 뒷면이 각각의 원소라고 할 수 있다.
예) 주사위의 경우 1, 2, 3, 4, 5, 6이 각각 원소가 된다.
- n 개의 표본점 w1, w2 ... wn으로 구성되어 있는 표본공간 Ω
다음과 같이 나타낸다.

근원사건
- 표본 공간에서 더 이상 쪼개질 수 없는 하나의 사건
- 표본공간의 한 원소만으로 이루어진 사건
- 예) {w1}, {w2}, {w3}
전사건
- 표본공간의 모든 원소를 포함하고 있는 사건
-주사위의 전사건은 1 ~6 모두.
공사건
- 아무것도 발생하지 않은 것
- 표본점을 하나도 포함하지 않는 사건
- 즉 집합인데 원소가 하나도 없는 것이다. = 공집합
1-2. 이산 표본공간과 연속 표본공간
이산 표본공간(무한하지만 셀 수 있는 것 - 정)
- 표본공간에 속하는 원소의 개수가 유한(이산)하거나
그 수를 셀 수 있는 경우
예) 주사위를 던지는 확률 실험에서의 관측값,
또는 어떤 공정에서 발생하는 불량품의 개수 등의 집합
연속 표본공간(무한하지만 셀 수 없는 것 - 실수)
- 표본공간에 속해 있는 원소가 실수의 구간으로 이루어져
있는 경우와 같이 수학적으로 셀 수 없는 경우
예) 어떤 공정에서 처음으로 불량품이 관측되는 시각
- 1시 25분 19초 (소수점 이하 쭈르륵)
예) 전구의 평균 수명 등의 집합은 연속 표본공간
- 전구를 샀는 데 꺼내자마자 전력 나가거나
전구를 샀더니 1년 쓰는 것, 혹은 2년 쓰는 것
2년 6개월 3일 쓰는 것 이렇게 수학적으로 셀 수 없게
무수히도 많이 쪼개릴 수 있는 경우
연습문제
1번. 주사위의 눈이 짝수가 나올 때까지
반복해서 던지는 실험에서 주사위를 던진 횟수에 대한 표본공간을 구하라
예) 처음 주사위를 던졌는데 4가 나왔다.
한 번 던졌더니 짝수가 나왔다.
이러면 표본공간 값은 1이 된다.
처음에 던졌는 데 3 나오고, 그 다음 5 나오고,
세 번째에 4가 나왔다. 던진 횟수는 3번이다.
표본공간은 3이 된다.
30번 던지고 31번째에 짝수가 나올 수도 있다.
이 문제의 답은 무한히 갈 수도 있다.
그래서 이 문제의 정답은 아래와 같다.
첫 번째: 짝
두 번째: 홀, 짝
세 번째: 홀, 홀, 짝
네 번째: 홀, 홀, 홀, 짝
이런 식으로 가면 다섯 번째, 여섯 번째 부터 무한까지도 가능하다.
표본공간은 S = { 1, 2, 3, 4 .... } 으로 이산표본공간이다.
* 이산표본공간(셀 수 있는 무한집합 or 자연수 전체집합)
2번. 1개의 동전을 반복해서
두 번 던지는 실험에 대한 표본공간을 구하고,
서로 다른 면이 나오는 사건 A를 구하라
발생 가능한 모든 경우는
'앞앞, 뒤뒤, 앞뒤, 뒤앞'이다.
즉 표본공간 S = { (앞, 앞), (앞, 뒤), (뒤, 앞), (뒤, 뒤) } 이다.
서로 다른 면은 (앞, 뒤), (뒤, 앞) 이므로
A = { (앞, 뒤), (뒤, 앞) } 이다.
3. 어느 공장에서 생상된 전구의 수명을 측정하는 실험을 할 때,
전구의 수명에 대한 표본공간을 구하라.
그리고 전구의 수명이 100시간 이상 200시간 미만일 사건
A의 표본공간을 구하라
전구를 샀는 데 운이 없어서
전구를 천장에 달자마자 전구가 깨지면서 불이 나가버렸다.
이런 경우 전구의 수명은 0이라고도 할 수 있다.
0이 아닌 1분 정도 불이 들어왔다가 전구의 수명이 다할 수도 있다.
이렇게 전구의 수명은 0초, 1초, 10분 9초, 3시간 12분 3초, 1년 등 다양하다.
즉 전구 수명의 표본공간은 실수 전체 집합라고 볼 수도 있다.
어떤 전구는 운이 좋아서 전구의 수명이 엄청 오래갈 수도 있으니까
실수 전체 집합이라고 표현했다.
위의 문제에선 전구의 수명을 100시간 이상 200시간 미만이라고 제한했다.
그러니 사건 A의 표본공간은 100 이상 200미만인 실수이므로
원소를 나열해서 나타낼 수는 없고, 범위의 조건을 제시해서 집합을 표현한다.
답: A = { 실수 X | 100 ≤ X < 200 }
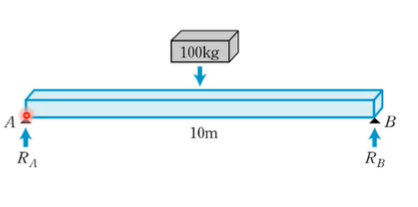
3. 다음 그림과 같이 길이가 10m이며,
양쪽 A와 B에 의해 받쳐져 있는 고른 재질의 평균대 위에 100kg의 물체가 놓인다고 하자.
두 지점 A, B는 단순 지지 역할만 하는 점이라고 하고,
A와 B가 받는 지지력(반력)을 각각 RA, RB라 할 때, 다음을 구하라.
(단, 물체가 평균대 위에 놓일 때 A와 B의 두 지점에서 받는 지지력의 합이
그 물체의 중량이 된다.)
(a) 100kg의 물체가 평균대 위에서 1m 간격으로 놓인다고 할 때,
지지력 RA, RB에 의해 이루어지는 표본공간을 구하고, 이를 그림으로 나타내라.
답: 100kg의 물체가 평균대 위에서
1m 간격으로 놓인다고 할 때, 평균대를 지지하는 반력 RA의 표본공간 ΩRA는 다음과 같다.
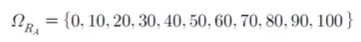
A랑 B가 총 부담해야 할 무게가 100인데
A가 10만큼 부담하면 나머지 90은 B가 부담해야 한다.
그래서 RA가 0만큼 부담할 때 즉 0일 때 RB는 100이다.
A가 0만큼 부담했으니까 나머지 100을 B가 부담하는 것이다.
RA가 10이면 RB는 90이 된다.
같은 방법으로 반력 RB도 같은 형태의 표본공간을 갖는다.
RB는 RA가 0일 때 100일 것이다.
즉 B 쪽에 얼마만큼 무게가 쏠리느냐에 따라
A가 부담해야 할 무게도 달라진다.
여기서 보면 알 수 있듯이
RA와 RB를 합친 것은 항상 100kg이다.
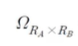
RA와 RB에 이루어지는 표본공간은
위와 같은 식으로 표현할 수 있다.
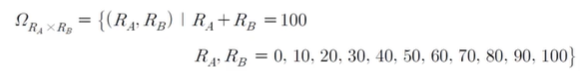
RA와 RB, 두 개의 쌍을 고려해서 집합을 만들 게 되면
위와 같이 만들 수 있다. RA와 RB의 쌍으로 나타낼 수 있는 값의 범위다.
RA + RB = 100이란 건 조건을 나타낸 거다.
RA와 RB를 더하면 100이라는 조건을 단 것이다.
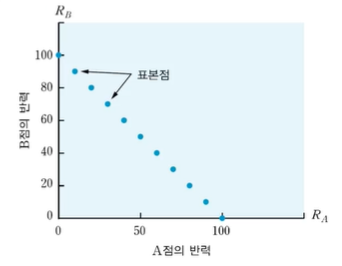
식을 그래프로 만들면 위와 같다.
RA가 0일 때 RB는 100이고,
RA가 10일 RB는 90인 것을 확인할 수 있다.
위의 점들은 표본공간을 이루고 있는 각각의 원소값이라고 할 수 있다.
위에처럼 점이 아닌 줄로도 나타낼 수 있다.
예를 들어서 중량 100kg의 물체가 평균대 위를 따라
A로부터 2m와 4m 사이의 어느 곳이든 놓일 수 있다면
RA의 표본공간은 다음과 같이 직선으로 나타난다.

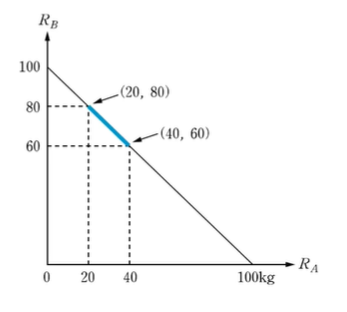
만일 RA가 20에서 40 사이인 사건을 생각하면
(RA, RB)에 대한 사건은 다음과 같이 (20, 80)과 (40, 60) 사이가 된다.
(b) 평균대 위에 놓이는 물체가 100kg에서
300kg 사이의 임의의 값을 가질 수 있고
평균대 위 어느 곳이든 놓일 수 있다면,
RA나 RB의 표본공간은 100kg에서 300kg 사이의 직선으로 나타난다.

(RA, RB)의 표본공간을 나타내면 다음과 같다.
그림에서 RA ≥ 200kg인 사건은 삼각형 형태이지만,
(RA ≤ 100, RB ≥ 100)인 사건은 사다리꼴 형태이다.
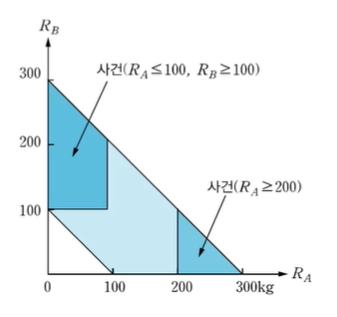
위의 그림이 표본공간이고
이 표본공간에 조건을 둠으로서 부분집합을 나타낼 수 있다.
가령 (RA ≤ 100, RB ≥ 100) 라는 조건을 뒀을 때의
해당 부분만 칠하면 위의 그림과 같은 부분집합을 나타낼 수 있다.
1-3. 사건의 연산
집합이 곧 사건이다.
사건의 연산도 결국 집합니다.
(1) 합사건
- 임의의 두 사건 A, B 중 적어도 한 사건이 일어나는 사건을
A와 B의 합사건이라 하며, 다음과 같이 나타낸다.
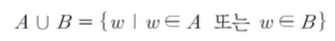
- A가 발생해도 돼고, B가 발생해도 돼고, 혹은 A와 B가 동시에 발생해도 된다.
(2) 곱사건
- 임의의 두 사 건 A, B가 동시에 일어나는 사건을
A와 B의 곱사건이라 하며, 다음과 같이 나타낸다.
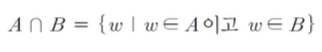
- 사건이 A 사건이면서 동시에 B 사건이어야 한다.
(3) 여사건
- 임의의 사건 A가 일어나지 않는 사건을
A의 여사건이라 하며, 다음과 같이 나타낸다.
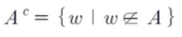
- 예) A 사건이 주사위를 던졌을 때 짝수가 나오는 사건이 A 사건이라면
2, 4, 6이 A 사건인데 A의 여사건은 짝수가 아닌 1, 3, 5가 된다.
(4) 배반사건
- 임의의 두 사건 A와 B의 곱사건(두 개 모두 만족)이
공사건(A 와 B가 동시에 만족되지 않는 것)일 때
즉 두 사건 A와 B가 동시에 일어나지 않을 때 A와 B는 서로 배반사건이다.
예) 동전 던지기를 해서 앞면이 나오면 A 사건,
뒷면이 나오면 B사건 이라고 했다.
내가 동전을 던졌을 때 앞면과 뒷면이 동시에 나타날 순 없다.
이런 경우를 A와 B는 배반사건이라고 한다.
사건의 연산 법칙

드로므간 법칙
- A와 B의 곱사건의 여사건은
각각의 A와 B의 여사건의 합사건과 같다고 볼 수 있다.
예제 2-5
1개의 주사위를 던지는 시행에서 짝수의 눈이 나오는 사건을 A,
홀수의 눈이 나오는 사건을 B,
3 이상의 수가 나오는 사건을 C라 하자.
(1) 표본공간 Ω를 정의하라
답: Ω = { 1, 2, 3, 4, 5, 6 }
(2) 근원사건, 전사건, 공사건을 각각 구하여라
답: 근원사건 > {1}, {2}, {3}, {4}, {5}, {6}
해설: 근원사건이란 표본공간의 한 원소만으로 이루어진 사건으로
사건이 집합인데 그 원소가 한 개만 있는 것이다.
답: 전사건 > { 1, 2, 3, 4, 5, 6 }
해설: 전사건이란 표본공간의 모든 원소를 포함하고 있는 사건
답: {}
해설: 공사건은 아무런 사건도 일어나지 않는 것을 의미
(3) A∪B와 B ∩ C를 각각 구하라.
답: A∪B = { 1, 2, 3, 4, 5, 6 } , B ∩ C = { 3, 5 }
해설: A = { 2, 4, 6 }, B = { 1, 3, 5 }, C = { 3, 4, 5, 6 } 이다.
A와 B의 합사건은 A와 B의 원소를 합치는 것으로
A∪B = { 1, 2, 3, 4, 5, 6 } 이다.
B와 C의 곱사건은 B와 C의 공통된 원소를 구하는 것으로
B ∩ C = { 3, 5 } 이다.
(4) A의 여사건을 구하라
답: A의 여사건 = { 1, 3, 5 }
해설: 해설: A = { 2, 4, 6 } 이니까 A에 포함되지 않는
1, 3, 5이 A의 여사건이다.
(5) A와 B가 서로 배반사건인지 아닌지를 판별하라
답: 배반사건이 맞다.
해설: 배반사건이란 서로 겹치는 게 없는지 확인하는 것이다.
즉 A와 B의 곱사건을 통해 서로 겹치는 게 없는지 확인하라는 거다.
예제 2-6
길이가 10m이며, 양쪽 A와 B에 의해 받쳐져 있는
고른 재질의 평균대 위에 놓이는 물체가 100kg에서
300kg 사이의 임의의 값을 가질 수 있고
평균대 위 어느 곳이든 놓일 수 있다면,
두 지점 A, B는 단순 지지 역할만 하는 점이라고 하고,
A와 B가 받는 지지력(반력)을 각각 RA, RB이다.
위의 표본공간에서 사건 A와 B가 다음과 같이 주어질 때,
두 사건의 합사건과 곱사건을 구하고, 이를 그림으로 나타내라.
A: RA ≥ 100kg, B: RB ≥ 100kg
정답:
A ∪ B = { ( RA, RB ) | (100 ≤ RA 또는 100 ≤ RB) 그리고 100 ≤ RA + RB ≤ 300 }
A ∩ B = { ( RA, RB ) | (100 ≤ RA 그리고 100 ≤ RB) 그리고 100 ≤ RA + RB ≤ 300 }
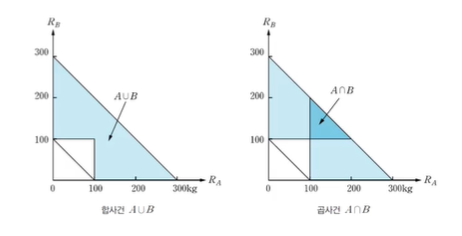
해설
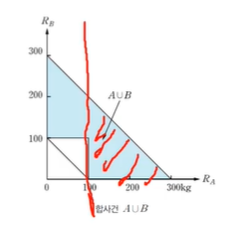
A는 100이상이니까 위에 칠한 것처럼 나타낼 수 있다.
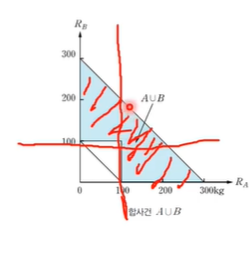
B도 100이상이라 했으니까 위의 그림처럼 칠할 수 있다.
A와 B의 영역을 모두 칠해주면 하늘색 부분이 된다.
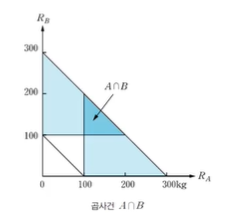
A와 B의 곱집합은 두 개의 영역에서
서로 겹치는 부분이기 때문에 진한 파랑색으로
칠해진 영역이 A와 B의 곱집합이라고 볼 수 있다.
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 조건부 확률, 곱셈 정리, 독립 사건이 뭘까? (0) | 2023.03.20 |
|---|---|
| [확통] 확률과 라플라스의 확률, 그리고 공리 (0) | 2023.03.09 |
| [확통] 왜 n!/(n-r)!은 nPr일까? (0) | 2021.12.31 |
| [확통] 왜 nPr(순열)에선 마지막에 n-r+1이 붙는 걸까? (0) | 2021.12.31 |
| [확통] 왜 표본분산 분모는 n이 아닌 n-1을 쓸까? (0) | 2021.12.29 |