이전에는 표본공간과 사건에 대해 알아봤다.
오늘은 확률에 대해 알아볼 예정이다.
<목차>
2. 확률
2-1. 라플라스의 확률
2-2. 확률의 공리
2-3. 확률의 성질
* 이공계생을 위한 확률과 통계를 참고해서 작성한 글입니다.
* 학교 수업 시간 때 들은 강의를 정리한 글입니다.
2. 확률
2-1. 라플라스의 확률(수학적 확률)
- 일반적으로 한 번의 시행에서 일어날 수 있는 경우의 수가 N인
근원사건(일어날 수 있는 사건의 원소값들)이 일어날 가능성이 같을 경우,
사건 A가 일어나는 경우의 수를 n이라 하면,
A의 확률은 다음과 같이 정의할 수 있다.
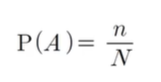
전체 표본공간인 N에
사건 A가 일어나는 경우의 수를 n이라 한다.
예) 주사위를 던졌는데
발생할 수 있는 경우의 수는 1 ~ 6 총 6가지다.
이러면 대문자 N은 6이 된다.
각 근원사건이 일어날 가능성이 같다는 건
주사위의 숫자 1, 2, 3, 4, 5, 6이 일어날 사건의 가능성(확률)이 같다.
1부터 6까지 나올 확률은 모두 6분의 1이다.
- 이러한 라플라스의 확률은 표본공간이 유한개의 표본점을 가질 때만
적용할 수 있으며, 각 근원사건이 일어날 가능성이 같지 않은 경우에는
사용할 수 없어 좀 더 일반적인 확률의 정의가 필요하다.
예) 현실 세계의 주사위는 완벽하지 않기에
주사위 숫자가 딱 6분의 1만큼 떨어져서 나오는 게 아닌
1이 좀 더 많이 나올 수 있고, 2나 5가 더 많이 나올 수도 있다.
라플라스의 확률은 논리적인 수학 세계에선 잘 적용되지만 현실세계에선 그렇지 않다.
이러한 라플라스의 한계를 확장하기 위해 '확률의 공리'가 등장했다.
2-2. 확률의 공리
- 각 근원사건이 일어날 가능성이 다른 경우와
주관에 따라 정하는 주관적 확률의 개념도 수용할 수 있는
확률의 공리(axiom of probability)를 정의
1) 확률의 공리 조건
다음 세 가지를 만족시키는 P(A)를 사건 A의 확률이라 한다.
(1) 표본공간 Ω에서 임의의 사건 A에 대하여 0 ≤ P(A) ≤ 1이다.
> 확률의 값은 1과 0 사이여야 한다.
(2) P(Ω) = 1 이다.
> 전사건(어떤 실험 했을 때 일어나는 전체 사건)의 확률은 1 이다.
(3) A1, A2, ....이 각각 서로 배반사건(서로 교집합 X) 이면 다음이 성립한다.
P( A1 ∪ A2 ∪ ... ) = P(A1) + P(A2) + ...
> 합사건은 각각의 확률을 더한 것과 같다.
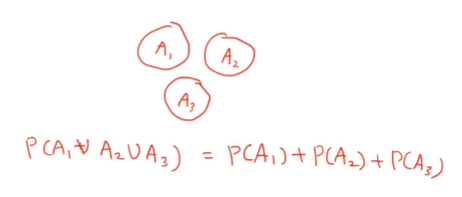
> 위의 그림처럼 서로 겹치지 않는 게 배반사건이다.
- 위의 확률의 공리로부터 유도되는
확률의 성질을 정리하면 아래와 같다.
2) 확률의 성질
- 확률의 공리로부터 유도되는
확률의 성질을 정리하면 다음과 같다.
(1) 공사건
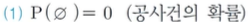
P의 공사건은 0이란 뜻이다.
공사건은 사건이 아무것도 일어나지 않는 걸 뜻하기 때문이다.
예) 내가 주사위를 던졌는 데 아무런 사건도 안 일어나진 않지 않는다.
(2) 여사건
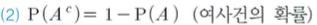
A의 여사건의 확률은 1 - (A)란 뜻이다.
즉 A가 일어나지 않을 확률은
전체(1)에서 A가 일어날 확률을 빼면
A가 일어나지 않을 확률이 나타난다는 것이다.
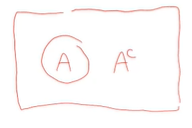
밴다이어그램을 그려서 생각해 보자면
A가 일어날 확률이 동그라미 내부라면
A가 일어나지 않을 확률인 나머지 AC는 그림과 같을 것이다.
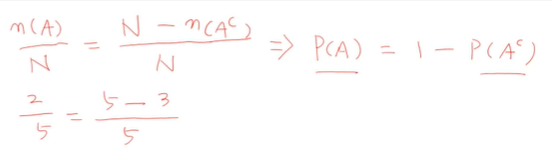
이를 식으로 표현하면 아래와 같다.
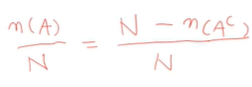
n(A)은 A에 포함된 원소의 개수를 의미한다.
n(Ac)는 A에 포함되지 않는 원소의 개수를 의미한다.
N은 전체 원소 개수, 즉 A에 포함되고, 포함되지 않는 원소를
다 합한 것이 N이다.
위의 식이 바로 이해가 가지 않을 수도 있을 거 같아
아래 그림을 추가했다.
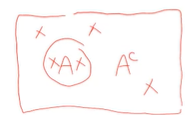
A의 원소 개수는 2개고,
A에 포함되지 않는 A의 여집합 원소 개수는 3개다.
전체 원소 개수(N)는 5개다.
이를 식으로 나타내면 아래와 같다.
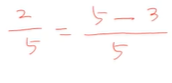
최종적으로 우리가 맨 처음에 본 식을 확인할 수 있다.
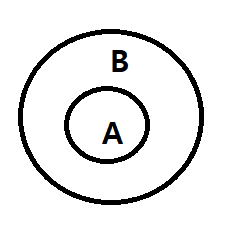
(3) 포함관계

A가 B에 포함된다면
A의 원소는 B의 원소와 같거나 작다.
그림으로 표현하자면 아래와 같다.
(4) 덧셈정리

A와 B의 합집합의 원소의 개수는
A와 B 원소를 더하고, A와 B의 교집합 개수를 뺀 것과 같다.
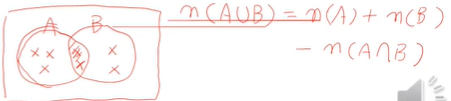
A 원소 개수가 5개
B 원소 개수가 4개다.
A와 B 원소를 더하면 9다.
이 9에서 A와 B의 교집합 원소 개수인 2를 빼면 7이다.
(5) 교집합이 0 이상일 경우
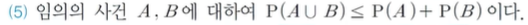
A와 B의 교집합이 0 이상이라면
P(A) + P(B) 부분이 더 크다.
3) 통계적 확률과 기하학적 확률
- 위에선 논리적으로 주사위 굴리면 6분의 1 확률로
각각의 숫자가 나온다고 했지만 생각에서 그치지 않고,
통계적인 실험을 여러 번 반복해서
실험의 결과로 해당되는 사건이 몇 번 일어나는지 알아보는 것이
통계적 확률이다.
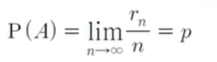
- 같은 시행을 n번 반복했을 때
사건 A가 일어나 횟수를 rn이라 하면,
n이 한없이 커짐에 따라 상대도수 n분의 rn이 일정한 값 p에
가까워짐이 알려져 있다.
이때 이 p의 값을 A의 통계적 확률이라 한다.
- n이 실험을 실행한 총 횟수를 의미한다.
- rn이 해당되는 사건, 즉 A 사건이 일어난 횟수를 의미
- n을 무한대로 보낸다는 건 전체 실험 횟수분에
A 사건이 일어 횟수를 나눠서 나타낸다.
- 표본공간과 사건 A가 무한집합이어서
그 수를 셈할 수 없는 경우가 있다.
예) 시행의 결과가 실수값인 경우를 의미한다.
전등의 수명은 3분 2.4455342초가 될 수 있다.
- 이럴 경우 다음과 같이 기하학적 확률을 적용한다.
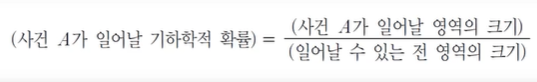
위의 식의 예로 원형 판을 돌려서
그 판에 화살을 던질 경우
원형 판이 전 영역의 크기가 돼고,
원형 판에 그려진 '꽝', '만원당첨', '인형담청'과 같은
특정한 사건이 일어날 영역이 될 수 있다?
예제 2-7
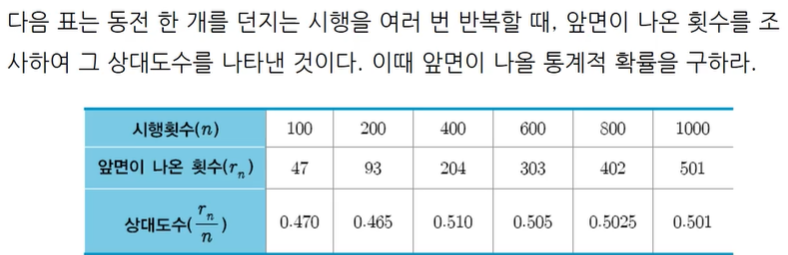
위의 표를 보니 100번 동전을 던졌을 땐
앞 면이 47번 나오고, 200번일 땐 93번 나온 걸 확인할 수 있다.
상대도수를 보면 갈수록 0.5에 가까워지는 걸 확인가능하다.

이걸 보고 알 수 있는 건 n이 무한대로 가게 될 경우
상대도수는 0.5가 될 거란 점이다.
사실 이건 당연한 건데
동전은 앞면 아니면 뒷면이라 이분의 일
즉 0.5일 수 밖에 없기도 하다.
예제 2-8
동전 한 개를 한 번 던지는 시행에 대하여 다음 물음에 답하라.
(a) 앞면과 뒷면이 나올 가능성이 동일하다고 할 때,
앞면과 뒷면이 나올 확률을 각각 구하고, 확률의 공리를 모두 만족함을 보여라.
> 공리를 만족한다는 건 어떤 사건이 일어날 확률이
0과 1 사이여야 하며, 시행 결과의 전체 집합은 1이어야 함과 동시에
두 사건이 서로 배반해야 공리이다.
* 배반: 동전 던질 때 앞면과 뒷면이 동시에 나오지 않는 것
확률의 공리 조건
다음 세 가지를 만족시키는 P(A)를 사건 A의 확률이라 한다.
(1) 표본공간 Ω에서 임의의 사건 A에 대하여 0 ≤ P(A) ≤ 1이다.
> 확률의 값은 1과 0 사이여야 한다.
(2) P(Ω) = 1 이다.
> 전사건(어떤 실험 했을 때 일어나는 전체 사건)의 확률은 1 이다.
(3) A1, A2, ....이 각각 서로 배반사건(서로 교집합 X) 이면 다음이 성립한다.
P( A1 ∪ A2 ∪ ... ) = P(A1) + P(A2) + ...
> 합사건은 각각의 확률을 더한 것과 같다.
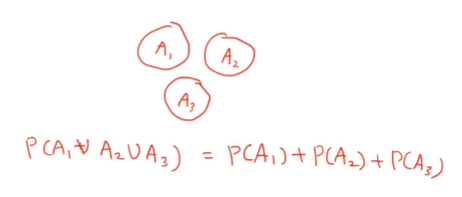
> 위의 그림처럼 서로 겹치지 않는 게 배반사건이다.
답:

- 동전을 던질 때 각각의 확률은 2분의 1로 0과 1 사이에서 확률이 발생
- 동전을 던졌을 때 앞면과 뒷면이 나올 확률은 각각 2분의 1로
이 모든 사건을 더하면 1이다.
- 동전을 던졌을 때 동시에 앞면과 뒷면이
나올 수는 없기에 각각의 사건은 배반사건이다.
(b) 앞면이 나올 가능성이 뒷면이 나올 가능성의 2배인
일그러진 동전이라 가정할 때, 앞면과 뒷면이 나올 확률을 각각 구하라.

해설:
뒷면이 나올 확률 P(T)를 X라고 하고,
앞면이 나올 확률은 뒷면이 나올 확률보다 두 배니까 P(H)는 2X가 된다.
두 개의 확률을 더한 건 전사건 1이어야 함으로
X + 2X = 1이어야 한다.
여기서 전사건이란 동전 앞면과 뒷면 나올 경우의 수 모두를 의미한다.
P(T∪H) = P(T) + P(H) 식으로 표현하면 이와 같고,
3X = 1 이기에 X = 3분의 1이다.
P(T)는 3분의 1이 되고,
P(H)는 뒷면이 나올 확률보다 두 배니
3분의 2가 된다.
예제 2-9
52장의 카드에서 한 장의 카드를 임의로 뽑을 때,
다음 사건의 확률을 구하라.
(a) 숫자 5카드가 나올 사건 A
답: P(A) = 52분에 4
(b) 다이아몬드 카드가 나올 사건 B
답: P(B) = 52분에 13
(c) 다이아몬드 그림의 A, K, Q, J 카드가 나올 사건 D
답: P(C) = 52분에 16
(d) 다이아몬드 그림의 A, K, Q, J 카드가 나올 사건 D
답: P(D) = 52분에 4

2-10
주사위 2개를 던져서 나오는 눈의 수를 순서쌍 (X1, X2)로 나타낼 때,
임의의 두 사건 A와 B가 다음을 만족한다. 주어진 확률(a~e)을 구하라.
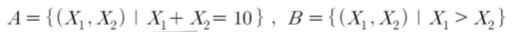
A는 주사위 눈 수 2개를 더했을 때 나오는 수가 10인 경우다.
B는 첫 번째 주사위가 두 번째 주사위 값보다 큰 경우다.
총 나올 수 있는 순서쌍은 36가지다.
(a) P(A)
답: A 사건의 경우의 수, 즉 2개의 숫자를 더했을 때
10이 되는 수는 (4,6), (5,5), (6,4)
총 3가지로 P(A) = 3/36 = 1/12이다.
(b) P(B)
답: B 사건의 경우의 수는 (2,1), (3,1), (3,2), (4,1),
(4,2), (4,3), (5,4), (5,3), (5,2), (5,1), (6,5), (6,4), (6,2), (6,1)
총 15가지이므로, P(B) = 15/36
(c) P(A∩B)
답: A와 B의 교집합은 (6,4) 한 개 뿐이다.
따라서 P(C) = 1/36이다.
(d) P(A∪B)
(e) P(Ac)
예제 2-11
실수 a가 -2 ≤ a ≤ 6을 만족할 때, x에 대한 방정식
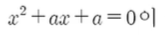
실근을 가질 확률을 구하라

실근을 가질 확률을 구하는 방법은
근의 공식에서 사용되는 b제곱 -4ac가 0 이상이면
실근을 가지고, 0이하면 허근을 가진다고 약속했다.
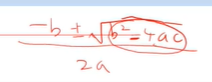
근의 공식은 위에처럼 생겼다.
근의 공식 안에 루트로 씌어진 부분인
b제곱 -4ac이 0보다 커야, 즉 양수여 근이 실수가 된다.
제곱햐소 마이너스가되는 실수는 없다.
그런 수는 허수라고 한다. 허수를 갖는 근을 허근이라고 한다.
이차방정식의 판별식을 이용하면
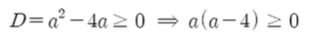
이다. 위의 식에서 근이 0과 4가 나온다.
0보다 작고, 4보다 클 경우 양수가 나온다고 할 수 있다.
즉 a ≤ 0 또는 a ≥ 4이다.
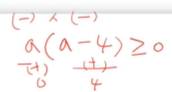
0보다 작을 경우 a(a-4) 양 측이 - -라 서 양수가 나올 수 있다.
4 이상일 경우 마찬가지로 양측이 + + 라서 양수가 나올 수 있다.

문제에서 a가 가질 수 있는 범위를 -2와 6 사이라고 했었다.
방정식이 실근을 가질 수 있는 조건은 0보다 작고, 4보다 커야 했음으로
위의 그림처럼 나타낼 수 있다.
주어진 방정식에 대한 실수 a의 조건은 다음을 만족한다.
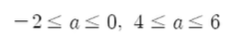
따라서 구하고자 하는 확률은 다음과 같다.

실근을 가질 a 범위의 길이의 경우
-2에서 0의 거리는 2이고,
4와 6 사이의 거리도 2이기 때문에
두 거리를 합하면 4가 된다.
예제 2-12

답:
전체 삼각형 밑변x높이는 300이다.
그리고 작은 삼각형은 100이다.
이를 식으로 표현하자면 아래와 같다.
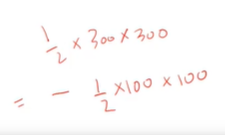
Q. 그런데 왜 나머지 작은 삼각형 100은 빼주지 않은 걸까?
그것도 지금 색이 칠해지지 않은 것으로 확인 됐는데?
> 문제 다시 한 번 꼼꼼히 읽어주기!
2-4(b)의 표본공간이라고 문제에서 말했었다.
해당 표본공간은
'평균대 위에 놓이는 물체의 중량이 100kg에서 300kg 사이의 임의의 값이고,
평균대 위 어느 곳에든 놓을 수 있다.' 이다.
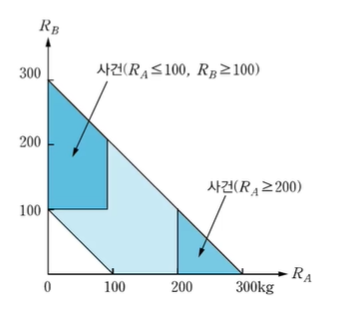
그림으로 표현하면 위와 같다.
그렇기에 작은 흰색 삼각형 또한 표본공간에 포함되는 게 맞다.

전체 면적은 40,000이다.

'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 배반 사건이 독립일 수 없는 이유 (0) | 2023.03.21 |
|---|---|
| [확통] 조건부 확률, 곱셈 정리, 독립 사건이 뭘까? (0) | 2023.03.20 |
| [확통] 표본공간이 무슨 뜻일까? (0) | 2023.03.09 |
| [확통] 왜 n!/(n-r)!은 nPr일까? (0) | 2021.12.31 |
| [확통] 왜 nPr(순열)에선 마지막에 n-r+1이 붙는 걸까? (0) | 2021.12.31 |