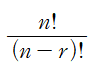
= nPr이다.
왜일까?
오늘은 그 이유에 대해 알아보려 한다.
1. 먼저 n!을 전개해보자.
n!을 전개하면
n! = n(n-1)(n-2)(n-3)...(n-r+1)(n-r)(n-r-1)...3X2X1 이 된다.
(보통 n!은 = n(n-1)(n-2)...3X2X1로 표현하거나
1X2X3....(n-2)(n-1)n로 표현하는데 위에 n! 식은 그걸 좀 더 상세히 풀어놓은 것이다.)
2. n!을 나눠보자.
n!을 /(슬래시) 로 끊어주려고 한다.
n! = n(n-1)(n-2)(n-3)...(n-r+1)/(n-r)(n-r-1)...3X2X1
즉 n!은 n(n-1)(n-2)(n-3)...(n-r+1)과
(n-r)(n-r-1)...3X2X1 으로 나눠졌다.
이렇게 2개로 나눠서 보니
‘n(n-1)(n-2)(n-3)...(n-r+1)’
이거 어디서 많이 본 것 같지 않은가?
바로 nPr의 공식이다.
nPr은 전개하면 ‘n(n-1)(n-2)(n-3)...(n-r+1)’ 로 나온다.
그럼 ‘n(n-1)(n-2)(n-3)...(n-r+1)’은 nPr이란 걸 머릿속에 담아두고
다음으로 넘어가자
(n-r)(n-r-1)...3X2X1은 뒤집어서
1X2X3...(n-r-1)(n-r)로도 표현해도 무방한데(5x4나 4x5나 결과값은 똑같은 것처럼)
즉 1부터 (n-r)까지 곱해준 거라고 볼 수 있다.
그렇다면 (n-r)!으로 표기가 가능하다.
n!을 생각하면 이해할 수 있다.
n!은 1부터 n까지의 수를 곱한 것이다.
예) n! = 1X2X3....n
1X2X3...(n-r-1)(n-r) 식에선 n대신 (n-r)이 들어간 것이고
즉 (n-r)! = 1x2x3....(n-r) 이 된다.
결론은 (n-r)(n-r-1)...3X2X1 = (n-r)!이라는 것이다.
처음으로 돌아와서 우리는 왜
nPr이 n!/(n-r)!인지를 알아내려고 했었는데
n!/(n-r)!은 아래와 같이 표현이 가능하다.
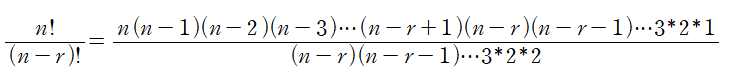
식을 보면 ‘(n-r)(n-r-1)...3*2*1’이 분모와 분자에 공통적으로 있는 것이 보일 것이다.
즉 (n-r)!이 분모 분자에 공통적으로 있는데 나누기로
분모, 분자에 있는 ‘(n-r)(n-r-1)...3*2*1’을 서로 지워주면
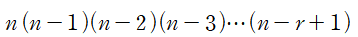
위의 사진과 같은 식만 남는다.
n(n-1)(n-2)(n-3)...(n-r+1)은 nPr의 공식이다.
결론적으로 n!을 (n-r)!으로 나눴더니 nPr만 남게 되었다.
이것이 n!/(n-r)!이 nPr인 이유다!
글이 조금이나마 도움이 되셨다면 공감(하트)버튼을 눌러주시면 감사하겠습니다!
공감은 글을 쓰는 데 큰 힘이 됩니다.
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 조건부 확률, 곱셈 정리, 독립 사건이 뭘까? (0) | 2023.03.20 |
|---|---|
| [확통] 확률과 라플라스의 확률, 그리고 공리 (0) | 2023.03.09 |
| [확통] 표본공간이 무슨 뜻일까? (0) | 2023.03.09 |
| [확통] 왜 nPr(순열)에선 마지막에 n-r+1이 붙는 걸까? (0) | 2021.12.31 |
| [확통] 왜 표본분산 분모는 n이 아닌 n-1을 쓸까? (0) | 2021.12.29 |