<목차>
4.1 이산확률분포
- 이산균등분포
- 베르누이 시행과 베르누이 분포
- 이항분포
4.2 연속확률분포
4.1 이산확률분포
- 이산균등분포
- 확률변수 X가 가지는 값(이산점)의 확률이
모두 같은 확률분포를 이산균등분포라고 한다.
예) 주사위 던지면 균등하게 1/6의 확률로 숫자가 나온다.
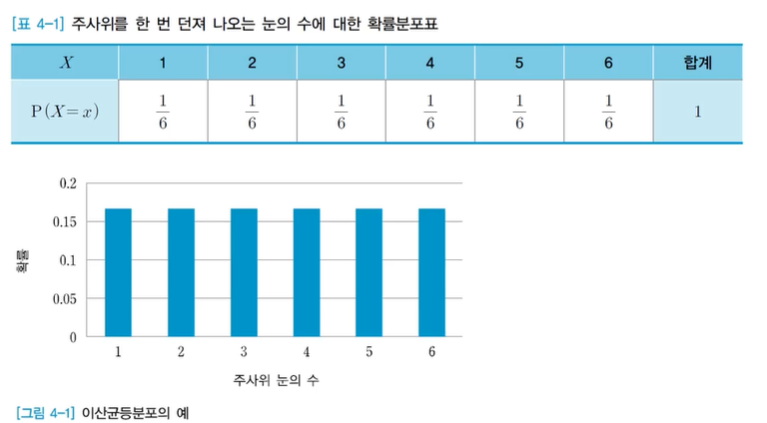
- 이산균등분포의 평균과 분산

예제 4-1

- 12달 중에 하나의 달에서 태어나니까 1/12가 된다.
- 평균(기댓값)으로 구할 수 있다.
베르누이 시행과 베르누이 분포
- 나오는 결과가 두 가지 밖에 없는 경우다.
- 동전 던지기를 하면 앞면이랑 뒷면 두 가지 경우 밖에 결과가 없다.
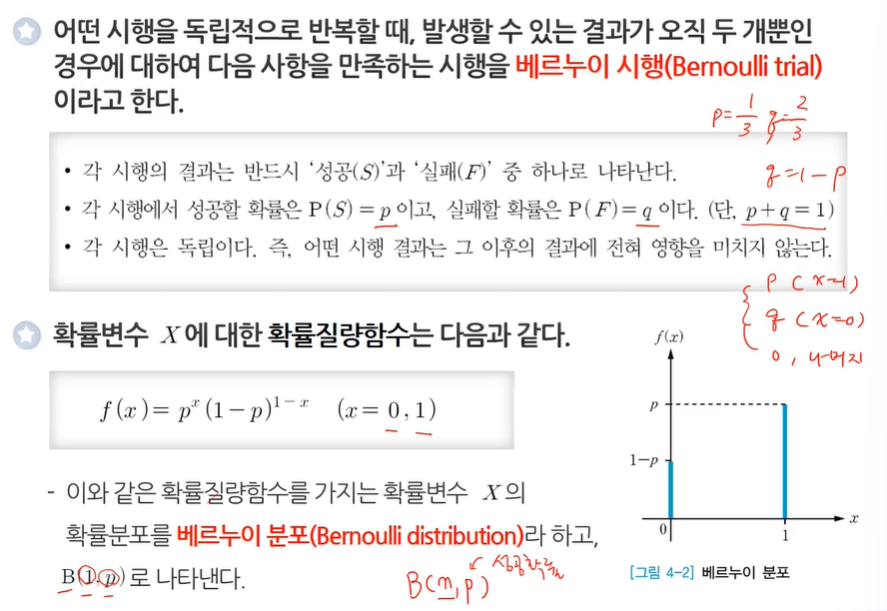
- B(1, p)에서 1은 횟수를 뜻하고, p는 성공확률을 뜻한다.
- 베르누이에서 실행은 1번만 있어서 1로 작성한다.

예제 4-2

10개의 제품 중 3개가 불량품이므로 불량품이 뽑힐 확률은 3/10
양품이 뽑힐 확률은 7/10이다.
또한 이때 추출하는 시행은 불량품이 뽑힐 확률이 3/10 또는
양품이 뽑힐 확률이 7/10인 베르누이시행이라고 한다.
예제 4-3

이항분포

- nC0 p^0 q^n에서 한 번도 성공하지 않을 확률은 0일 확률이다.
- 즉 nC0이 n번 중에서 한 번도 성공하지 못한 경우다.
- P는 성공확률인데 여기선 0번 성공했으니 P^0이다.
- 나머지 n번은 다 실패해서 q^n이다.


베르누이일 때와는 다르다.
예제 4-4

중간에 (1/4)^1은 틀렸다.
(1/4)^3이 정확하다.
결과로는
((5*4)/2) * ((3^2)/(4^5)) = 45/512
예제 4-5

예제 4-6

(a) 불량품이 2개 나올 확률을 구하라

(b) 이항분포표를 이용하여 불량품이 최소한 3개일 확률을 구하라.
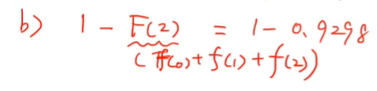
최소 3개 이하일 확률은 반대로 생각하면
전체에서 2개일 확률, 1개일 확률, 0개일 확률을 빼주면
최소 3개 이하일 확률을 구할 수 있다.
(c) 확률변수 X의 기댓값과 분산을 각각 구하라.
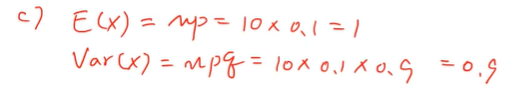

초기하분포

- NCn : 대문자 N에서 소문자 n만큼 뽑는다.
- MCx: 성공한 개수가 M이고, 그 중에서 x개가 뽑혔다.
- N-MCn-x: 나머지 N-M개 중에서 소문자 x개만큼 뽑아간다.

N은 전체고, M은 전체 안에 있는 성공한 개수다.
M/N은 전체 공 중 양품을 뽑을 확률, 성공할 확률이라고 생각하면 된다.

@ 앞에 뭐 생략
- 25개 중에서 5개를 뽑는데 결합이 없다고 했으니 P(X<=0)이다.
- 0이 곧 위에서 말했던 c다.
- M값(불량률)이 무엇인지에 따라서 성공확률(p)도 달라진다.
- M이 0 즉 불량이 하나도 없다면 성공확률은 100%다.
- M이 1 하나가 불량이라면 확률이 80%로 떨어진다.
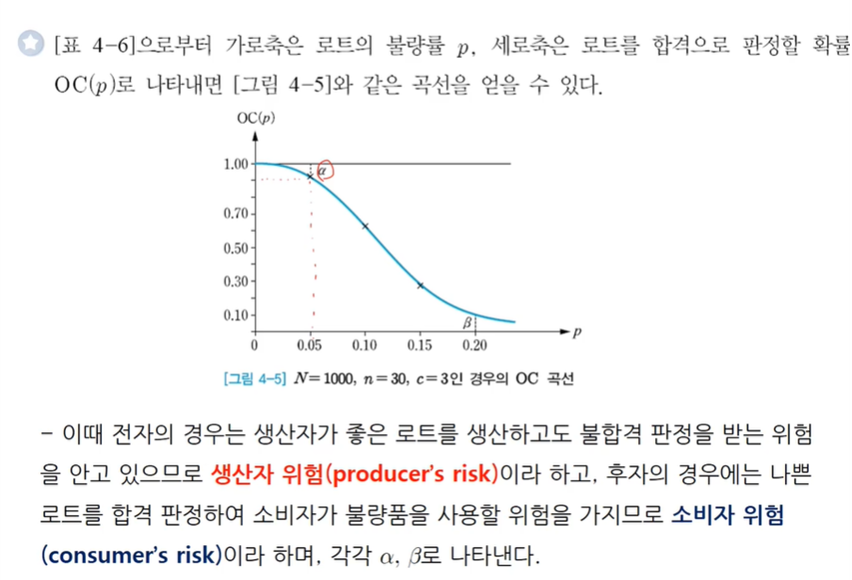
예제 4-7

예제 4-8

- X ~ B(5, 0.1)은 이게 이항분포라면
5번을 뽑는데 그중에서 불량품이 뽑힐 확률이 10/100이니까 0.1이다.
- 여기서 성공확률은 불량품이 뽑힐 확률이라서 성공확률 자리에 불량품 확률을 넣어준 것
- 확률질량함수가 5니까 5Cx 다.
- f(x) 식을 가지고, f(1)과 1-f(0)을 구해야 하는 문제다.
푸아송분포

- 전체 구간을 n개로 나누고 그 n개 중에서
사건 m번이 발생한다. 그래서 m/n이다.

푸아송 분포의 분포함수

푸아송분포의 평균과 분산

예제 4-9

- 한 시간에 1통의 전화를 받는다고 했으니 m = 1이다.
- 확률질량 함수는 첫 줄처럼 표현 가능
- x가 2통인 경우를 구한다고 했으니 두 번째 줄처럼 구할 수 있다.
예제 4-10

(a) 결함이 있는 제품이 1개 이하로 나올 확률을 구하라
- 1000개 중에서 결함이 10개라고 했으니 P = 10/1000이다.
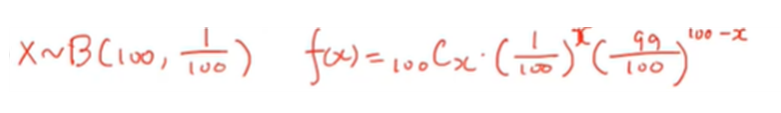
- 이항분포라고 생각하면 100개를 뽑는데 오류가 날 확률이 1/100이니 B(100, 1/100)이다.
- 확률질량함수 f(x)는 다음과 같다.
- 이항분포하려면 계산이 복잡하니까
f(0) + f(1)을 하면 a의 답을 구할 수 있다.
(b) 푸아송분포표를 이용하여 결함이 있는 제품이 최소 4개일 확률을 구하라
4개 이하일 확률을 구하라는 말은
다르게 보면 전체에서 3개 이하일 확률을 빼면 구할 수 있는 확률이다.

- x가 3이고, n이 1.0인 거가 표에서 0.981이라고 나와있다.
P(X => 24) = 1-P(X <= 3)
(C) X의 기댓값과 분산을 구하라.
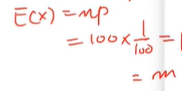
이항분포로 본다면 위에처럼 풀 수 있다.
포하송 분포의 경우 위에처럼 풀 수 있다.

포하송 분포는 기댓값과 분산 모두 값이 같고 m이 1이라 정답은 1이 된다.
예제 4-11

- x는 2개 이하일 확률을 구해야 한다.
- 확률질량함수는 1000개의 부품 중 100개를 뽑으려고 한다.
- 불량(M) 개수 중에서 x개를 뽑고,
- 정상은 1000개에서 -M개를 빼고, 100-X를 작성해주면 된다.
- x는 2이하이기 때문에 0, 1, 2다.
- m은 선택되는 평균값
- m = np = 100*p이다.
- m대신 100p를 넣어줬다.
- 이후부턴 부록 참고 필요.
183~187 안 중요해서 제외하고, 연속확률분포로 넘어
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 표본분포이 뭘까? (0) | 2023.05.16 |
|---|---|
| [확통] 연속활률분포 - 균등분포가 뭘까? (0) | 2023.05.07 |
| [확통] 공분산과 상관계수 (0) | 2023.04.21 |
| [확통] 결합확률분포가 뭘까? - 7weeks (0) | 2023.04.21 |
| [확통] 확률변수의 기댓값과 분산 (0) | 2023.04.11 |