[목차]
5.1 모집단과 표본분포
5.2 표본평균의 분포
5.3 여러 가지 표본분포
5.4 표본평균의 차의 분포
5.5 표본비율의 분포
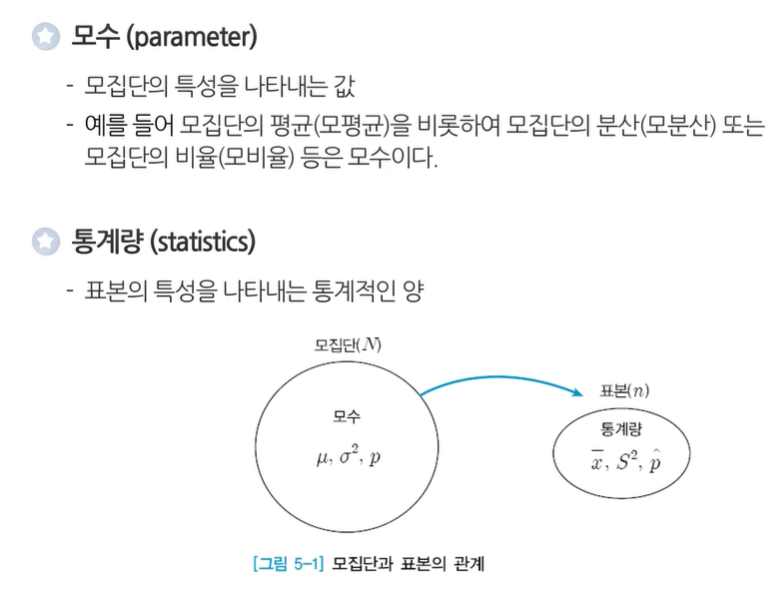
5.1 모집단과 표본분포
- 모집단은 통계조사 대상 전체를 말한다.
- 모집단을 모두 조사하는 걸 전수조사라고 한다.
- 전체 중에서 몇 개를 표본으로 추출하여 조사하는데,
이러한 자료에 대한 확률분포를 표본푼포라 한다.
- 표본추출에는 반드시 오차가 따르기 마련인데
이러한 오차를 표본오차라고 한다.
- 응답자가 정확하게 응답을 하지 않아 발생하는 비표본오차도 존재한다.
예) a가 원래는 b라는 후보 좋아하는데 c라는 후보가 좋다고 답하는 경우
확률추출법
- 샘플을 어떤 기준으로 잡을 것인지에 대한 것
예) 투표 샘플 뽑을 때 특정 지역 사람들만 대상으로 해서 뽑으면 왜곡이 발생할 수 밖에 없다.
- 모집단의 개체가 표본으로 뽑힐 가능성이 모두 동등하다는 조건에서
객관적으로 표본을 추출하는 방법
- 임의 추출법이라고도 한다.
- 확률추출법에 의하여 추출된 표본을 확률표본 또는 임의표본이라고 한다.
Skip 비확률추출법부터 확률추출법 종류(모두 다 생략)
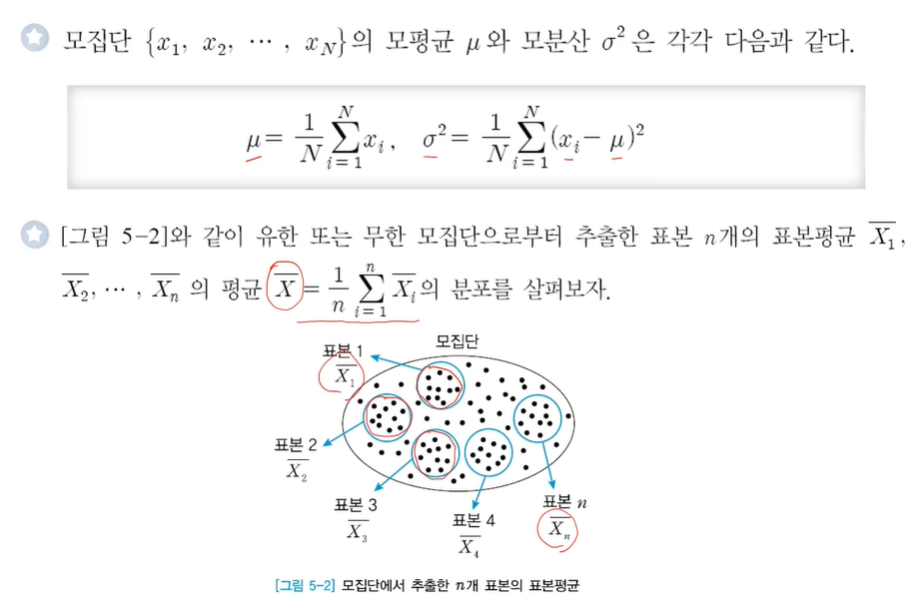
5.2 표본평균의 분포
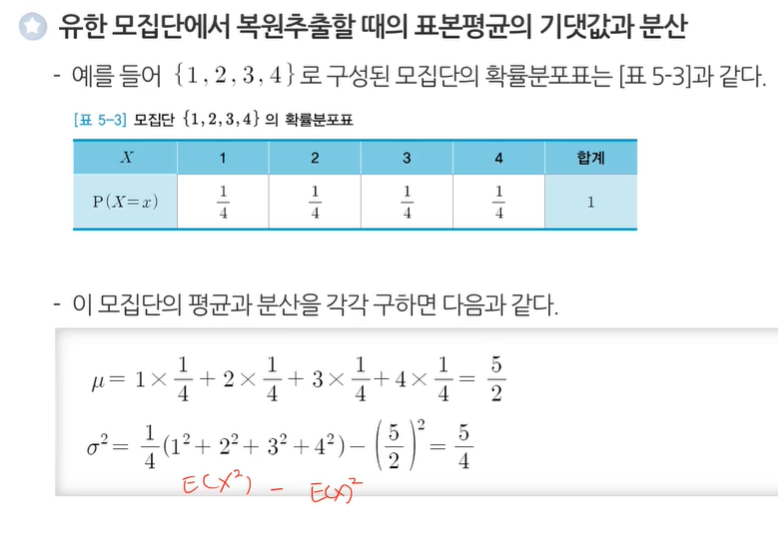
유한 모집단에서 복원추출할 경우 표본평균의 기댓값과 분산

예시

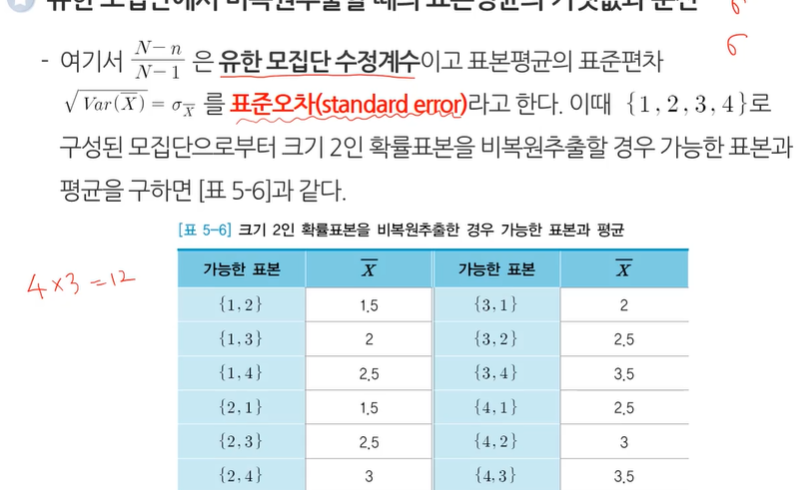
- 위에선 복원추출의 경우이고,
비복원추출할 경우를 생각해 보자.

- 평균은 값이 똑같다.
- 분산은 모집단의 크기가 N이 소문자 n이 표본의 크기다.
- N으로 이루어진 건 수정계수라고 한다.
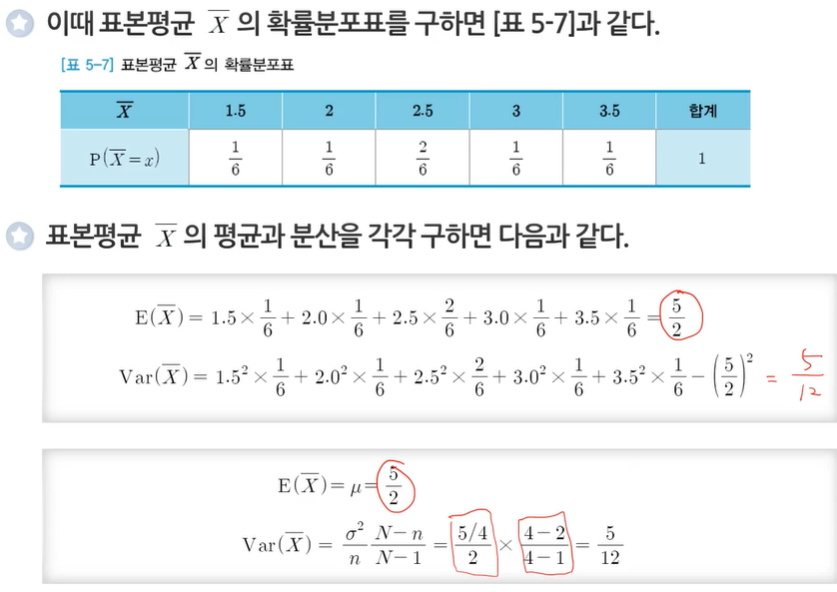
무한 모집단에서 비복원추출할 때의 표본평균의 분포

- n 값이 무한으로 간다고 하면 수정계수는 1로 수렴하게 된다.
- 분산을 구하면 n분에 시그마 제곱이 된다.
추출률

- 모집단에 비해서 표본이 작은 경우, 유한 모집단이라 하더라도 수정 계수가 1에 가깝다.
예제 5-1

예제 5-3 (5-2 skip)

- 모집단: 1,000, 평균(M): 100g, 분산(시그마): 5g, 표본(n): 50
- 표본평균의 평균은 M이다
- 표분평균의 분산은 n분의 시그마 제곱이다.
- 아래는 비복원
- 분산이 n분의 시그마 제곱 곱하기 수정계수 필요
예제 5-4


- 표본평균에서 모평균을 뺀 것의 차이가 200이하라는 것
- 이것의 확률을 구해야 한다.

'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 연속활률분포 - 균등분포가 뭘까? (0) | 2023.05.07 |
|---|---|
| [확통] 확률분포 종류 (0) | 2023.05.02 |
| [확통] 공분산과 상관계수 (0) | 2023.04.21 |
| [확통] 결합확률분포가 뭘까? - 7weeks (0) | 2023.04.21 |
| [확통] 확률변수의 기댓값과 분산 (0) | 2023.04.11 |