1. 확률변수
2. 확률분포
3. 확률변수의 기댓값과 분산
4. 결합확률분포
5. 공분산과 상관계수
3. 확률변수의 기댓값과 분산
확률변수 X의 기댓값
- 평균을 구하는 걸 기댓값 구하는 거라고 생각하면 된다.
- 확률변수 X의 기댓값 E(X)는 다음과 같이 정의한다.

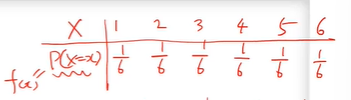
이산확률변수는 주사위를 던질 때 1이 나올 확률,
2가 나올 확률, 3이 나올 확률 모두 1/6이 나온다.
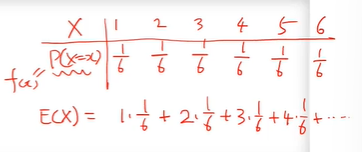
여기서 기댓값(E(X))을 구하려면
나올 값과 그 값이 나올 확률을 곱해서 모두 더해주면 된다.
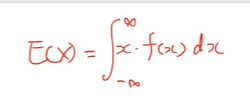
확률밀도함수는 곱해서 적분하면 된다.
예제 3-13
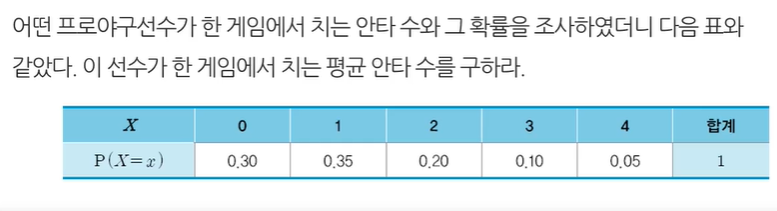
풀이

기대값은 뮤라고 쓰기도 한다.
- 확률변수에 대한 기댓값은 위에처럼 표현할 수 있다.
- x 대신 2x + 1 이렇게 함수로 주어진 기대값이 얼마냐고 물어보면
기댓값의 성질

(1) 해설
실험을 했는 데 계속 3만 나오는 경우
기대값을 3 즉 상수 k라고 할 수 있다.
(2) E(kX) = kE(X)
- 확률변수 X에 k를 곱한 거다.
- 이는 k를 바깥에 두고 곱한 것과 같다.
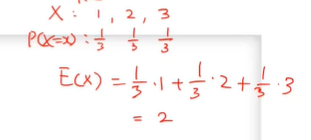
- 예) X가 1, 2, 3 균등하게 나온다면
위에처럼 작성해서 기대값을 구할 수 있다.

- 만약 k가 2, 4, 6이었을 때 결과값은
위에서 작성했던 E(x) 식에 k배 여기선 2배 한 것과 같다.
(3) E(X + k) = E(X) + k
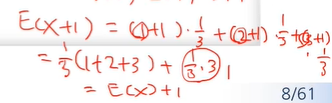
확률변수에 상수(k)를 더하는 것은
X의 기대값(E(X))에 상수 k를 더한 것과 같다.
예제 3-14
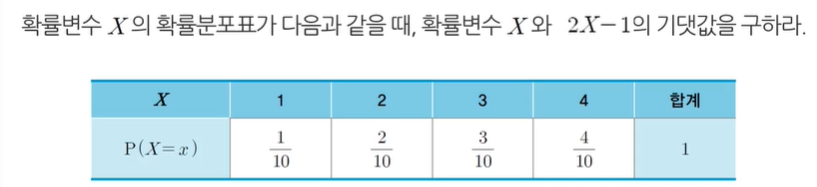
풀이
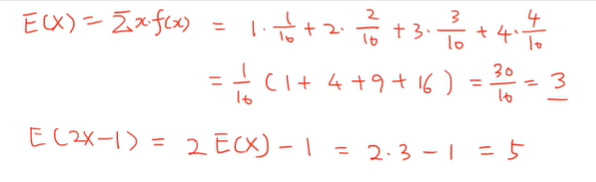
예제 3-15

(a) 풀이
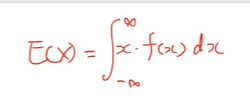
확률밀도함수의 기댓값을 구하기 위해선 위의 식을 활용하면 된다.
적분해서 x를 곱해주는 형태다.
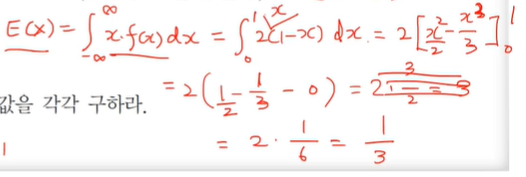
(b)
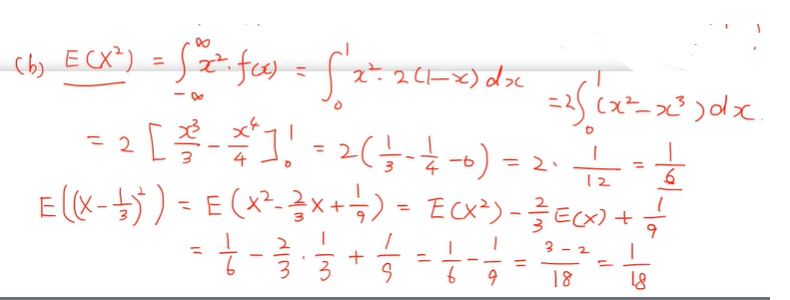
- x 대신 x^2를 넣어서 계산해주면 된다.
확률변수의 분산

- 분산은 각 값에 평균을 빼고 제곱을 하면 된다.
- 평균(뮤)는 E(x) 기댓값이라고도 한다.


- 분산을 구하라고 하면 확률 변수의 제곱에서 평균의 제곱을 배면 된다.
- 여기서 평균은 E(X)^2과 같다.
- 평균은 기댓값과 같다고 보기 때문이다.
예제 3-16

- 3-13에서 구한 기댓값은 1.25였다.
분산의 성질

(1) 해석
- 상수에 대한 분산은 항상 0이다.
- k가 3이라고 한다면 항상 3이 나올 것이고, 평균은 3이 된다.
- 상수 3에 평균 3 빼면 0나온다.
(2) 해석
- 변수에 상수(k)를 더하거나 빼도 분산에는 영향을 주지 못한다.
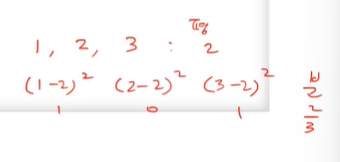
- 1, 2, 3 총 3개의 데이터가 있다고 하자.
- 평균은 2가 된다.
- 분산은 2/3가 된다.
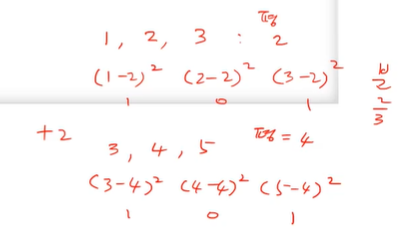
- 여기서 변수에 +2를 해주면
1은 3이 될 것이고, 2는 4, 3은 5가 된다.
- 이 상태로 분산 구해도 1, 0, 1 그대로다.
- 결국 상수를 더하거나 빼는 것은 분산에 영향을 주지 않는다.
(3) 해석
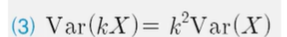
- 확률변수에 k를 곱하면
X분산에 대해서 k를 제곱하는 것과 같다.
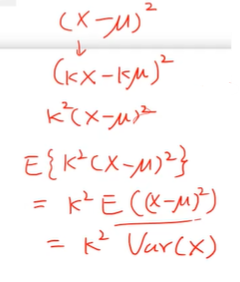
- 분산은 변수에 평균 뺀 값을 제곱한 것이다.
- x가 kx로 바꼈다면 평균에도 k를 붙여줘야 한다.
예제 3-17
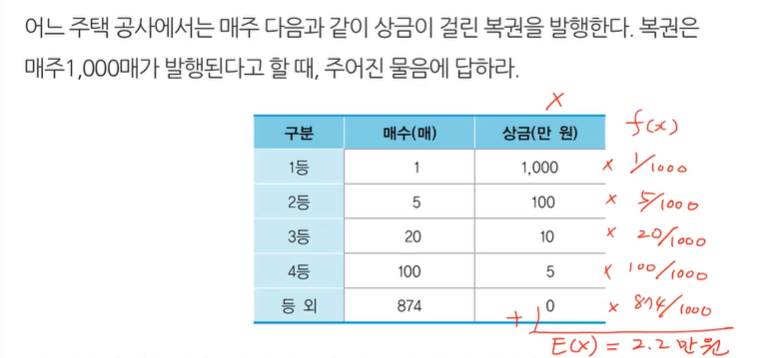
(a) 복권 한 장을 임의로 사서 받는 상금을 X라 할 때,
확률변수 X의 기댓값을 구하라.
E(X) = 1000*1/1000 + 100*5/1000 + 10 * 20/1000 + 5*100/1000 + 0*874/1000 = 2.2 만원
(b) 확률변수 X의 분산을 구하라.
- Var(X) = E(X^2) - E(X)^2
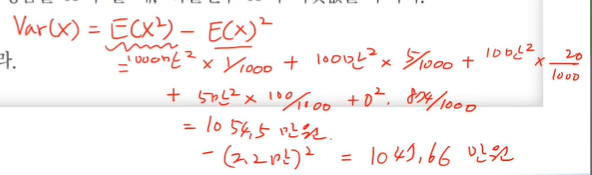
(c) 확률변수 X의 표준편차를 구하라.
표준편차는 분산에서 루트 씌어주면 된다.
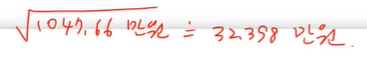
예제 3-18
예제 3-8에서 6개월 후에 작동 가능한
불도저 대수의 기댓값과 분산을 각각 구하라
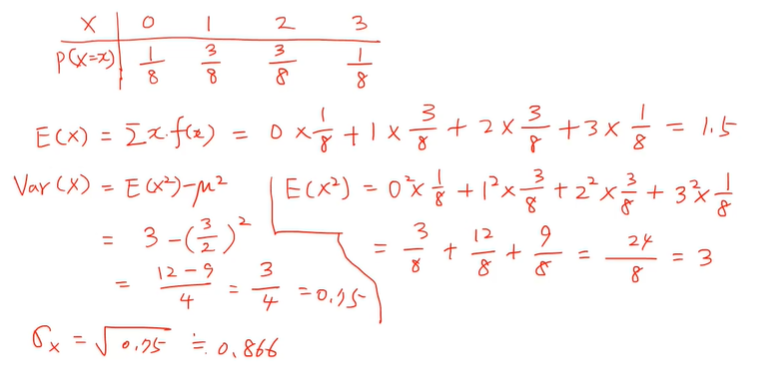
- 분산은 제곱의 평균에서 평균의 제곱을 빼면 된다.
- 평균은 1.5고 3/2로 표혀할 수도 있다.
- 분산은 0.75가 나온다.
적률생성함수


예제 3-20 생략하심
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 공분산과 상관계수 (0) | 2023.04.21 |
|---|---|
| [확통] 결합확률분포가 뭘까? - 7weeks (0) | 2023.04.21 |
| [확통] 확률밀도함수 (0) | 2023.04.02 |
| [확통] 확률변수 (0) | 2023.03.27 |
| [확통] 베이즈 정리 (0) | 2023.03.27 |