<목표>
1. 결합확률분포
2. 결합확률밀도함수
결합확률분포 정의
- 하나의 확률변수에 대해서 보통 생각한다.
- 예) 주사위 던졌을 때 주사위 눈의 값을 X라 하자.
- 이 X가 확률변수 X가 된다.
- 이때 X의 값이 1이 나올 확률, 2가 나올 확률을 구한다.
- 결합확률분포는 다르다.
- 확률변수가 한 개만 있는 게 아니라 두 개가 있다.
- 확률변수가 X와 Y가 있단 식이다.
- 예) 주사위와 동전 던지기를 동시에 시행한다.
동전이 앞면이 나오고, 주사위는 2가 나왔다고 했을 때
동전이 앞면이 나올 땐 X가 0, 뒷면이 나올 땐 1이라고 한다면,
Y는 주사위 눈의 값(1~6)이라고 한다면
동전에 의한 값인 0과 1과 주사위에 의한 1~6의 값이 쌍을 이루게 된다.
- 이것들의 확률변수의 확률분포 값을 고려하는 것이다.
- 위에서처럼 동전이 앞면이 나오면서 주사위가 2가 나오는 경우를 고려할 수 있다.

- 확률변수 X만의 혹은 Y만의 확률분포는 1차원적인 거다.
- 영어와 수학성적이 쌍으로 되어있는데(결합분포)
- 수학은 고려하지 않고, 영어만 고려한다고 했을 때
- 하나의 확률변수만 고려하고, 나머지는 고려하지 않는다고 본다.
- 이를 두고 X의 주변분포라고 이야기한다.
- 정리하자면 영어, 수학 점수 다 고려한다면 결합확률질량함수고,
영어만 따진다면 주변확률질량함수인 것이다.

- 마이너스 무한대에서 X까지,
- 마이너스 무한대에서 Y까지 다 더해서 얻어진 값을 결합분포함수라고 한다.
결합확률질량함수의 성질

(1) 해석
- 확률 값이라 0 이상이어야 한다.
(2) 해석
- 전사건에 대한 확률은 1이다.
(3) 해석
- 범위가 주어졌다면 그 범위에 해당하는 값만 더해준다.
예제 3-21

(a) 두 확률변수 X와 Y의 결합확률질량함수를 구하라
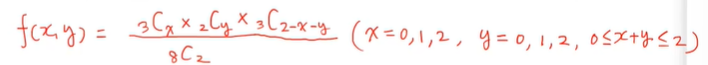
- 공 8개 중에서 2개를 뽑는다고 한다.
- 파랑 공 3개 중에서 x개를 뽑았다.
- 붉은 공 2개 중에서 y개를 뽑았다.
- 초록 공 3개 중에서 2-x-y를 빼주면 된다.
만약 파랑 공 한 개, 붉은 공 0개를 뽑았다면
초록공은 1개가 뽑힌 건데 2-x-y 식을 이용하면 그렇게 나온다.
- X의 경우 붉은 공을 하나도 못 뽑거나, 1개만 뽑거나 2개를 뽑을 수 있음으로
- X = 0, 1, 2가 나올 수 있다. Y도 마찬가지다.
- 총 2개를 뽑는 거라 X와 Y를 더한 것은 2를 넘을 수 없다.
(b) 두 확률변수 X와 Y의 결합확률분포표를 작성하라

위의 식처럼 x와 y의 경우의 수를 고려해서 식을 구하면 된다.
이 식을 표로 표현하면 아래와 같다.
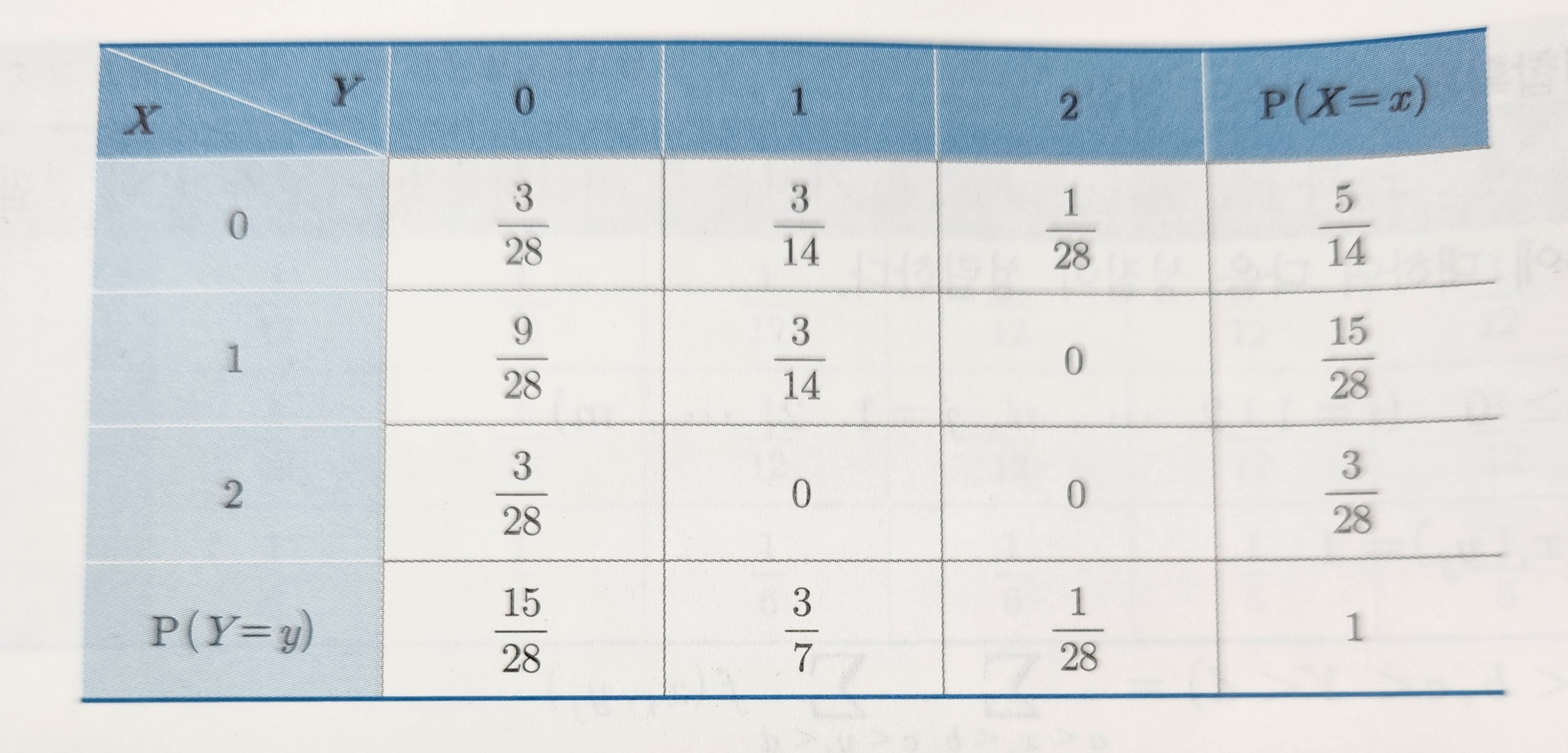
- f(x)부분의 경우 첫 째줄에는 x가 0인 경우인
3/28, 3/14, 1/28을 모두 더한 수가 들어간다.
- x가 1인 부분엔 15/28이 들어간다. 9+6은 15니까.
(c) P(X + Y + <= 1)을 구하라
- x와 y를 더했을 때 1 이하인 건 총 3가지 경우다.
- (0,0), (0,1), (1,0)이다.
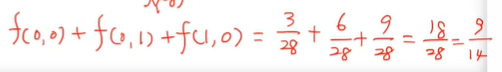
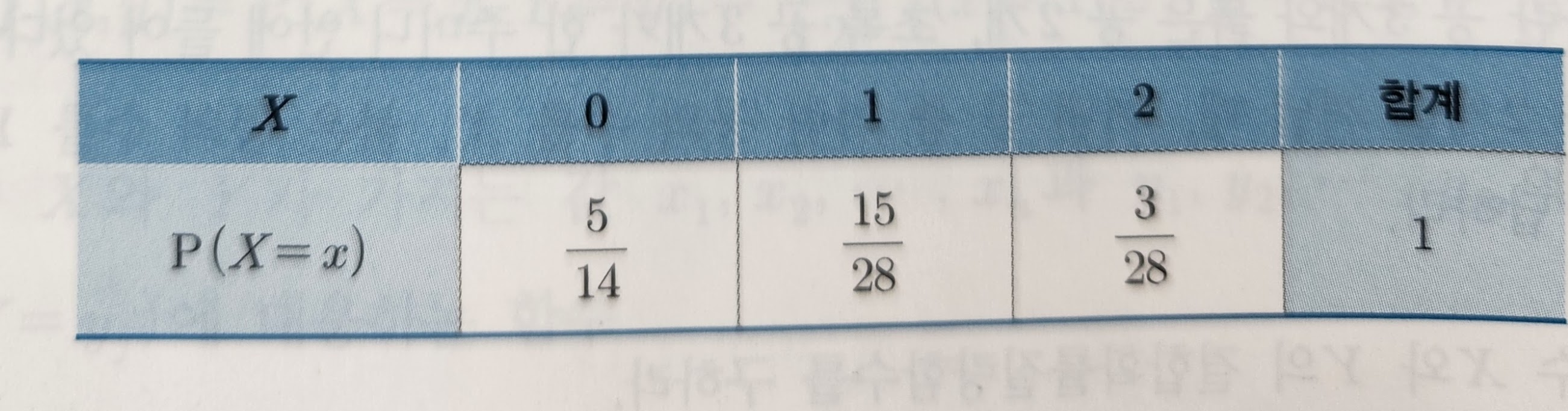
(d) 확률변수 X의 주변확률질량함수를 표로 작성하라
(e) 확률변수 Y의 주변확률질량함수를 표로 작성하라

(f) P(X<=1)을 구하라.
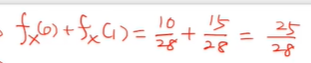
(g) P(Y<=1)을 구하라.
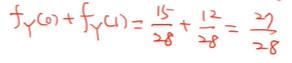
2. 결합확률밀도함수
- 두 개 이상의 확률변수가 결합되어 있는 걸 연속확률분포라고 했다.
확률이 분포되어 있는 정도를 나타낸 걸 결합확률밀도함수라고 한다.
- 확률변수가 한 개일땐 확률밀도함수라 했지만
두 개일 땐 결합확률밀도함수라고 한다.

(2) 해석
x에 대해서 먼저 적분하고,
y에 대해서 적분하면 그 결과값이 1이다.
(3) 해석
X와 Y가 A 안에 포함되는 거라면
그 영역에 포함되는 확률을 구하라.

- x에 대해서만 구하거나
y에 대해서만 구할 때 주변확률밀도함수라고 한다.
- x에 대한 주변확률밀도함수 값을 구한다 했을 때
y값이 무엇이든 상관없으니까
전체 y값에 대해서 적분을 해주면 된다.
결합확률밀도함수를 적분하면?

결합확률밀도함수의 성질

(2) 해설
- 전 범위에서 적분한 건 1이여야 한다.
예제 3-22

(a) 상수 a를 구하라
- 전 범위를 적분하면 1이다란 성질 이용
- x랑 y랑 0 이상에서부터 값을 가지기 때문에 0에서 무한대, 0에서 무한대라고 작성 가능
- 익스포네이션은 a*e^-x&e^-y와 같다.
- 익스포네이션이라 throw away!
- 7 weeks
(b) 확률변수 X의 주변확률밀도함수 fx(x)를 구하라
(c) 확률변수 Y의 주변확률밀도함수 fy(y)를 구하라
(d) P(0<=X<=1, 0<=Y<=1)을 구하라
(e) P(0<=X<=1)을 구하라
(f) P(0<=Y<=1)을 구하라
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 확률분포 종류 (0) | 2023.05.02 |
|---|---|
| [확통] 공분산과 상관계수 (0) | 2023.04.21 |
| [확통] 확률변수의 기댓값과 분산 (0) | 2023.04.11 |
| [확통] 확률밀도함수 (0) | 2023.04.02 |
| [확통] 확률변수 (0) | 2023.03.27 |