1. 확률변수
- 이산활률 변수
- 연속확률변수
- 확률질량 함수
2. 확률분포
확률변수의 기댓값과 분산
결합확률분포
공분산과 상관계수
확률밀도함수
- 이산확률변수 일 때는 확률질량함수로 나타낼 수 있다. <더해주는 것
- 연속확률변수 일 때는 확률밀도함수로 나타낼 수 있다. <적분해주는 것

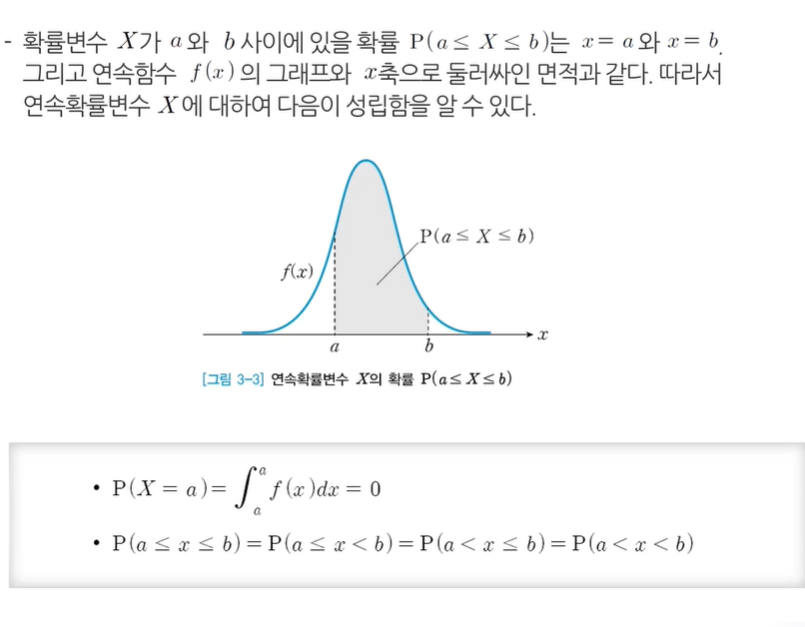
- x라 a에서 b 사이에서 분포할 확률(P)을 구해라
- a와 b 범위를 확률밀도함수를 적분해줘야 한다.
확률밀도함수의 성질

(1) 해석
- f(x)가 음수가 될 수 없다는 이야기다.
확률은 마이너스가 나올 수 없다.
(2) 해석
- 마이너스 무한대에서 플러스 무한대 즉
전 범위에서 확률밀도함수를 적분하면 1이다.
전사건이라고도 볼 수 있어서다.
(3) 해석
a에서 b 범위에 들어가는 연속확률변수 X가
a에서 b 범위 안에 들어갈 확률분포를 구하라고 하면
그건 a에서 b 범위 안에서 적분을 해주면 된다.
- 적분을 a에서 a로 하는 건 시작과 끝이 같은 거라 결과값이 0이 나온다.
예제 3-5

- 0과 1사이 외에는 확률이 존재하고
그 외에는 0이라 했음으로
0과 1사이에서만 확률이 존재한다는 거다.
- 0은 적분해도 0이다
- 0에서 1사이의 값이 전체 확률(1)이 된다.
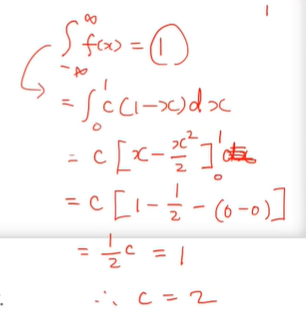
- c는 상수라서 앞으로 나온다.
- 1 - x를 적분하면 각각 x - x^2/2가 나온다.
- 적분방법
- x에 1을 넣은 거에서 x에 0을 넣은 걸 빼주면 된다.
- 정답: 2
(b) 해석
- 상수 c는 위에서 2라는 걸 알아냈다.
- 확률 P(0<X<1/2) 사이에 있을 때 f(x) = 2(1 - x)의 값을 구해야 한다.

- 1/2와 0 사이에서 적분을 하면 된다.
- 정답은 3/4가 된다.
2. 확률분포
- 다음과 같은 함수(F(x))를 확률변수 X의 분포함수라 한다.
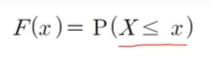
- X가 소문자 x보다 이하일 확률을 구하라
누적분포함수
- 이산확률변수 X의 분포함수는 임의의 실수 x에 대하여
이산확률변수 X가 x보다 작거나 같은 값을 취하는 확률로 정의하므로,
분포함수 F(x)를 누적분포함수라고도 한다.

분포함수의 성질

(2) 해석
- 확률질량함수를 모두 더하기 때문에 증가함수다.
(3) 해석
- 무한대까지 다 더했다는 이야기는
마이너스와 플러스 모두 다 더했다는 이야기다
- 전 실수 범위에선 1이 된다.
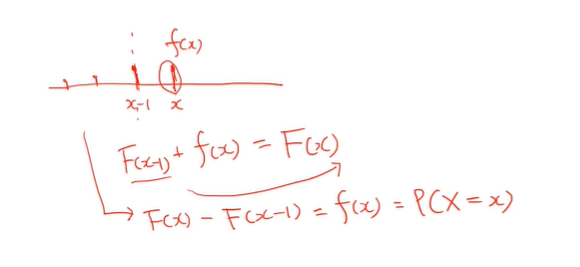
- 마이너스 무한대까지만 했다는 건
시작지점을 적분한들 값이 없다고 했다.
- x가 5라고 했을 때 x-1은 4다.
처음부터 5까지의 수에서 처음부터 4까지의 수를 빼면
특정 한 지점의 값 즉 f(x)가 나온다.
예제 3-6

- x < 0이 0이라는 건
0 이하로부턴 확률이 없다는 이야기다.
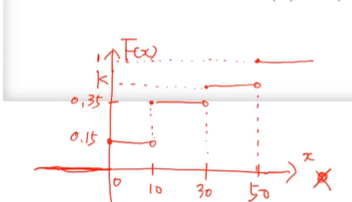
- 위의 식을 그림으로 나타내면 위와같다.
- 0부터 10 사이에서 0.15라고 했음으로
해당 지점에선 확률이 존재한다는 거다.
- 마지막에 50에서 1이 나왔다는 건 확률분포가 끝났다는 거다.
- 확률이 존재하는 지점은 0, 10, 30, 50이다.
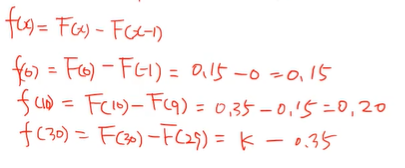
- f(0), f(10), f(30)은 위의 식을 통해서 구할 수 있다.
- f(56) = F(50) - F(49) = 1 - k이다.
- 문제에서 구하고자 하는 것은
P(30 <= X <= 50)이었다.
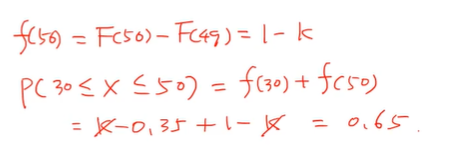
- f(30) + f(50)을 구하면
30과 50 사이의 이산확률변수인 X를 구할 수 있다.
- 정답: 0.65
예제 3-7
서로 다른 동전 2개를 동시에 던지는 실험에서 앞면이 나오는 횟수를
확률변수 X라 할 때 주어진 물음에 답하라.

(a)
서로 다른 동전을 던졌을 때 나오는 경우의 수는
(앞, 앞), (앞, 뒤), (뒤, 앞), (뒤, 뒤) 총 4가지다.
앞면이 나오는 횟수를 확률변수 X라 했음으로
(앞, 앞) = 2, (앞, 뒤) = 1, (뒤, 앞) = 1, (뒤, 뒤) = 0이다.
x가 한 번도 안 나올 확률은 전체 4 중에서
1번(뒤, 뒤)이다. x가 한 번 나올 확률은 전체 4 중에서
(앞, 뒤), (뒤, 앞) 총 2번임으로 2/4 = 1/2이다.
이렇게 구해진 게 확률질량함수가 된다.
분포함수를 구하라고 문제에서 말했음으로 분포함수를 구해보자.

- 0보다 작은 경우에는 항상 0 이다.
- 0이 되는 순간 1/4이다.
- 0에서 시작해서 1이 되기 전까지는 1/4이다.
- 1이 되면 1/4에 1/2가 더해진다.
그래서 1부터 시작해서 2 직전까지는 3/4이다.
- 2가 되는 순간에는 3/4에 1/4이 더해진다. 그래서 1이 된다.
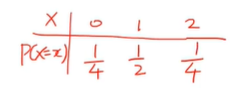
(b) 확률변수 X의 확률질량함수를 막대그래프와
확률 히스토그램으로 표현하라
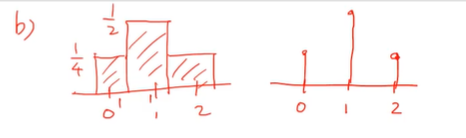
- 0일 땐 1/4이다.
- 1일 땐 1/2이다.
- 2일 땐 1/4이다.
첫 번째가 히스토그램, 두 번째가 막대그래프다.
(c) 확률변수 X의 분포함수를 그래프로 표현하라
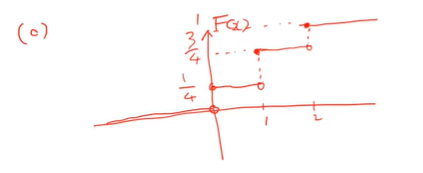
예제 3-8


- 3대가 모두 양호할 확률,
- 2대만 양호할 확률, 1대만 양호할 확률
하나도 양호하지 않을 확률을 위에 그림을 통해 구할 수 있다.
- 전체 개수는 8이다.
이를 확률분포표로 나타내면 아래와 같다.
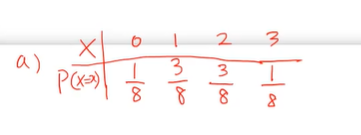
(b) 확률변수 X의 분포함수를 구하고, 그 그래프를 그려라
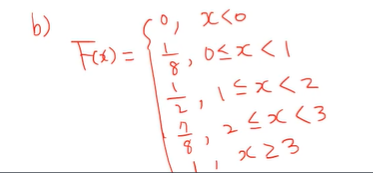
확률분포 함수를 그리면 위와 같다.
이를 토대로 그래프를 그리면 아래와 같다.

연속확률분포
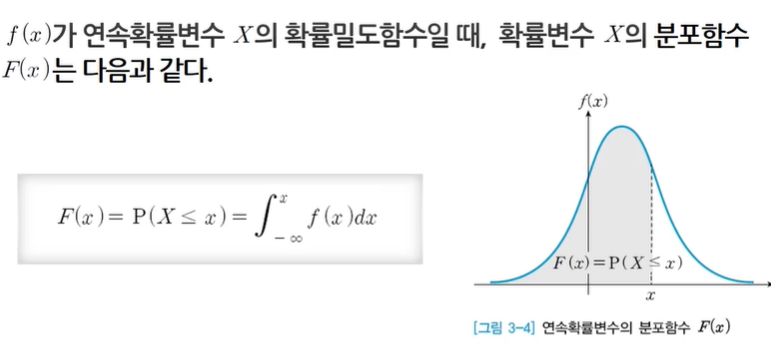
확률밀도함수는 적분을 통해서 구한다고 했었다.
연속확률분포일 때는 F(x) 즉 미분한 걸
f(x) 즉 적분하는 것으로 바꾸는 것이다?

분포함수를 이용하여 연속확률변수 X가 구간에 있을 확률을 구할 수 있다.
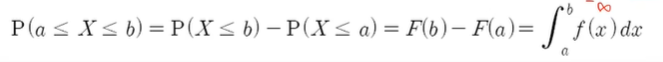
P(X<=b) - P(X<=a)를 그림으로 표현하면 아래와 같다.
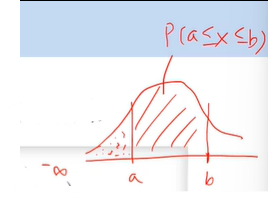
- 빗금친 부분을 구하기 위해선
마이너스 무한대에서 b까지 접근한 거에서
마이너스 무한대에서 a까지의 부분을 빼면
a와 b 사이를 구할 수 있다.
예제 3-9

(a) P(1 <= X <= 1.5) 즉 X가 1에서 1.5 사이일 확률을 구하라 한다.
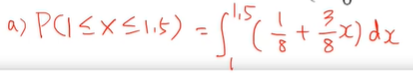
- 1과 1.5는 0과 2 사이에 있는 것이라
1/8 + 3/8x를 적분해주면 된다.
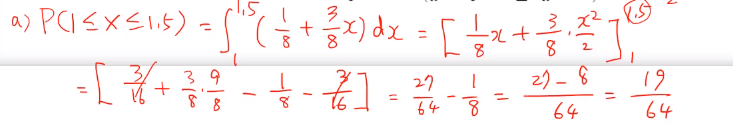
1.5를 분수로 나타내면 3/2이다.
이를 염두해두고 풀면 된다.
(b) P(X > 1)를 구하라
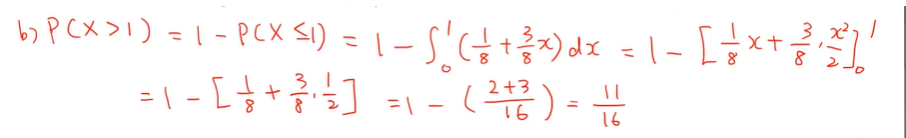
- 위의 문제는 1 - P(X <=1)로도 볼 수 있다.
- 1 이하는 마이너스 무한대에서 1까지 적분하는 건데
실제 함수의 값이 있는 경우가 0 이하는 값이 없어서,
0에서부터 1까지 구하면 된다.
예제 3-10

(a) 상수 c를 구하라
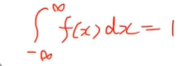
- 전범위의 성질을 알아야 한다.
- 전범위는 언제나 1이다.
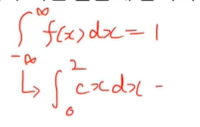
위의 문제에서 0 이하 2 이상은 모두 0이라서
이 문제에서 전범위는 0과 2사이로 구할 수 있다.
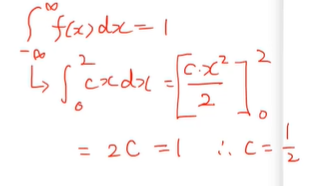
- 0과 2사이에 있는 cx를 적분하면 위와같이 표현할 수 있다.
(b) 확률변수 X의 분포함수를 구하라
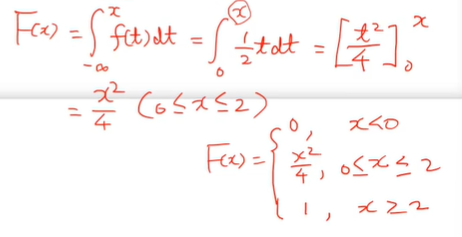
- 현재 f(x) = 1/2x ( 0 <= x <= 2)이다.
- 분포함수를 구하기 위해선 F(x)를 적분하면 되고
범위는 -무한대에서 x까지 적분한다.
- 적분할 때 1/2tdt에서 뒤에있는 dt는 없는 셈 취급한다.
(c) P (- 2 < X < 1 )을 구하라
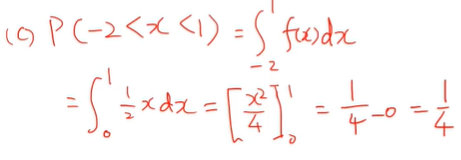
1에서 -2 사이에서 적분하란 이야기지만
0 이하로는 확률이 0이라서 1에서 0 사이로 적분하란 이야기와 똑같다.
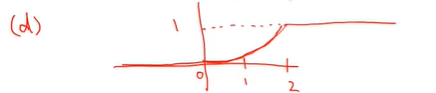
(d) 확률변수 X의 분포함수 그래프를 그려라
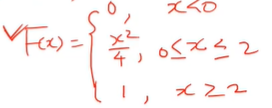
위의 분포함수를 토대로 아래와 같은 그래프를 그리면 된다.
예제 3-11
확률밀도함수의 값은 변함이 없다.
100kg이라는 똑같은 물체를 이동만 시키는 거이기 때문.
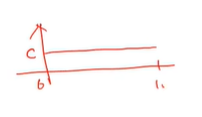
그림으로 표현하면 위와 같다.

확률밀도함수 f(x)는 위와 같고
c를 적분하면 아래와 같다.
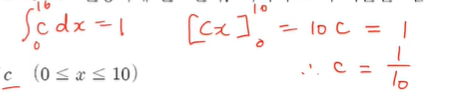
분포함수를 구하는 방법은 아래 공식을 통해 구할 수 있다.
도대체 왜?
나는 c가 1/50으로 나온다.
c 뒤의 dx는 곱해주지 않는 dx다.
그래서 x^2같은 게 없다.
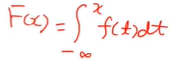
f(x)가 연속확률변수 X의 확률밀도함수일 때
확률변수 X의 분포함수 F(x)는 위과 같다.
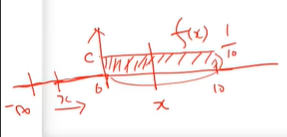
마이너스 무한대에서
어떤 X라는 지점까지 있을 때
0이하부터는 확률값이 없으니까 0부터 X까지 적분을 해주면 된다.
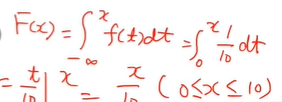
예제 3-12 @ ★ - 시험에 나옴

- F(x)는 누적분포함수를 뜻한다.
- x가 0 이하일 땐 0이다.
- 0보다 클 땐 1-e ^-x. 여기서 e는 2.8을 뜻한다.

- x가 커지면 분모가 커지는 거라 값이 점점 작아지게 된다.
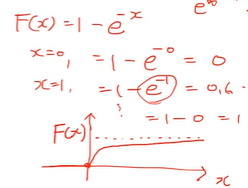
x = 0일 때 0, x = 1일 때 0.6 이렇게 x의 값이 커질수록 e^-x의 값은 작아지고,
이 값이 작아질 수록 1 - e^-x의 값은 1에 가까워진다.
(a) 확률변수 X의 분포함수를 이용하여 P(3 < X < 5)를 구하라.
P(3 < X < 5)를 구하란 말은
확률분포함수 P ( a < X < b) = F(b) - F(a)로 구할 수 있다.
b 분포함수에서 a 분포함수를 빼는 것이다.
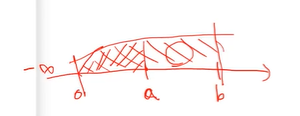
그림으로 나타내면 동그라미 친 부분을 구해야 하는 것이다.
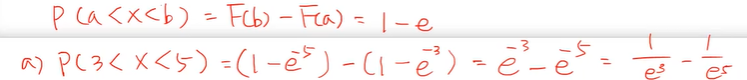
(b) 확률변수 X의 확률밀도함수를 이용하여 P(3 < X < 5)를 구하라.
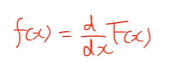
- 확률밀도함수는 위의 식처럼
확률분포함수를 미분해서 구할 수 있다.
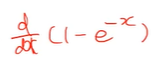
- (1-e^-x)를 미분하면 위에처럼 표현할 수 있다.

- 익스포네이션 e^x를 미분하면 자기 자신이다.
적분해도 자기자신이 나온다.
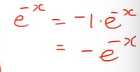
- e^-x를 미분하면 위에처럼 나온다.
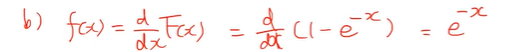
- 1은 상수고 상수를 미분하면 0이 된다.
- -e^-x를 미분하면 e^-x가 나온다.
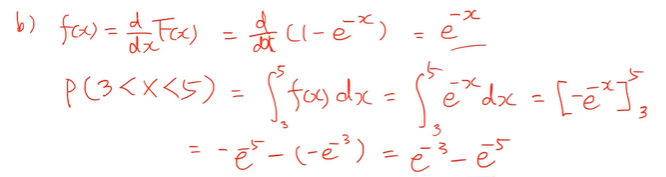
확률밀도함수를 3과 5사이에서 적분해주면 된다.
'Math > 확률과 통계' 카테고리의 다른 글
| [확통] 결합확률분포가 뭘까? - 7weeks (0) | 2023.04.21 |
|---|---|
| [확통] 확률변수의 기댓값과 분산 (0) | 2023.04.11 |
| [확통] 확률변수 (0) | 2023.03.27 |
| [확통] 베이즈 정리 (0) | 2023.03.27 |
| [확통] 배반 사건이 독립일 수 없는 이유 (0) | 2023.03.21 |